Advertisements
Advertisements
प्रश्न
A point OI in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D. Prove that OB2 + OD2 = OC2 + OA2
उत्तर
Let ABCD be the given rectangle and let O be a point within it.
Join OA, OB, OC and OD.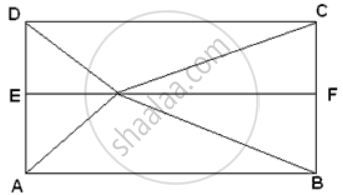
Through O, draw EOF || AB. Then, ABFE is a rectangle.
In right triangles ΔOEA and ΔOFC, we have
OA2 = OE2 + AE2 and OC2 = OF2 + CF2
⇒ OA2 + OC2 = (OE2 + AE2) + (OF2 + CF2)
⇒ OA2 + OC2 = OE2 + OF2 + AE2 + CF2 ......(i)
Now, in right triangles OFB and ODE, we have
OB2 = OF2 + FB2 and OD2 = OE2 + DE2
⇒ OB2 + OD2 = (OF2 + FB2) + (OE2 + DE2)
⇒ OB2 + OD2 = OE2 + OF2 + DE2 + BF2
⇒ OB2 + OD2 = OE2 + OF2 + CF2 + AE2 [∵ DE = CF and AE = BF]....(ii)
From (i) and (ii), we get
OA2 + OC2 = OB2 + OD2.
APPEARS IN
संबंधित प्रश्न
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
In a right triangle ABC right-angled at C, P and Q are the points on the sides CA and CB respectively, which divide these sides in the ratio 2 : 1. Prove that
`(i) 9 AQ^2 = 9 AC^2 + 4 BC^2`
`(ii) 9 BP^2 = 9 BC^2 + 4 AC^2`
`(iii) 9 (AQ^2 + BP^2 ) = 13 AB^2`
PQR is a triangle right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)
In ∆PQR, point S is the midpoint of side QR. If PQ = 11, PR = 17, PS = 13, find QR.
A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

In ∆ ABC, AD ⊥ BC.
Prove that AC2 = AB2 +BC2 − 2BC x BD
Find the Pythagorean triplet from among the following set of numbers.
2, 6, 7
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
Two poles of height 9m and 14m stand on a plane ground. If the distance between their 12m, find the distance between their tops.
The perpendicular PS on the base QR of a ∆PQR intersects QR at S, such that QS = 3 SR. Prove that 2PQ2 = 2PR2 + QR2
An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height
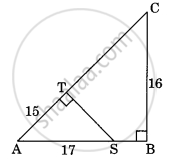
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is ______.

For going to a city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
