Advertisements
Advertisements
प्रश्न
Two poles of height 9m and 14m stand on a plane ground. If the distance between their 12m, find the distance between their tops.
उत्तर
Let AB and CD be the two poles of height 14m and 9m respectively.
It is given that BD = 12m
∴ CE = 12m
Now,
AE = AB - BE
= 14m - 9m = 5m
Using Pythagoras theorem in ΔACE,
AC2 = AE2 + CE2
= (5m)2 + (12m)2
= 25m2 = 144m2
= 169m2
= 13m2
⇒ AC = 13m
Thus, the distance between the tops of the poles is 13m.
APPEARS IN
संबंधित प्रश्न
Side of a triangle is given, determine it is a right triangle.
`(2a – 1) cm, 2\sqrt { 2a } cm, and (2a + 1) cm`
In a right triangle ABC right-angled at C, P and Q are the points on the sides CA and CB respectively, which divide these sides in the ratio 2 : 1. Prove that
`(i) 9 AQ^2 = 9 AC^2 + 4 BC^2`
`(ii) 9 BP^2 = 9 BC^2 + 4 AC^2`
`(iii) 9 (AQ^2 + BP^2 ) = 13 AB^2`
Tick the correct answer and justify: In ΔABC, AB = `6sqrt3` cm, AC = 12 cm and BC = 6 cm.
The angle B is:
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

`"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is
(A)\[7 + \sqrt{5}\]
(B) 5
(C) 10
(D) 12
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
Find the value of (sin2 33 + sin2 57°)
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

The sides of the triangle are given below. Find out which one is the right-angled triangle?
40, 20, 30
To get from point A to point B you must avoid walking through a pond. You must walk 34 m south and 41 m east. To the nearest meter, how many meters would be saved if it were possible to make a way through the pond?
If in a ΔPQR, PR2 = PQ2 + QR2, then the right angle of ∆PQR is at the vertex ________
Find the unknown side in the following triangles
Find the unknown side in the following triangles
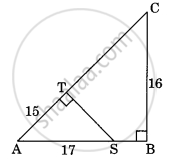
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
In a triangle, sum of squares of two sides is equal to the square of the third side.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
