Advertisements
Advertisements
प्रश्न
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9AQ2 = 9AC2 + 4BC2
उत्तर
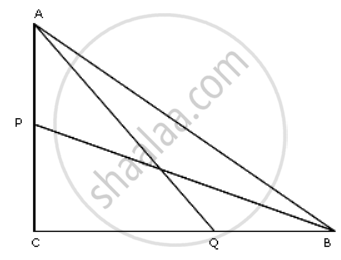
P divides AC in the ratio 2 : 1
So C.P. = `(2)/(3) "AC"` .......(i)
Q divides BC in the ratio 2 : 1
QC = `(2)/(3)"BC"` ......(ii)
In ΔACQ
Using Pythagoras Theorem we have,
AQ2 + AC2 + CQ2
⇒ AQ2 = `"AC"^2 + (4)/(9)"BC"^2` ...(using (ii))
⇒ 9AQ2 = 9AC2 + 4BC2. ......(iii)
APPEARS IN
संबंधित प्रश्न
The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right traingle ,right-angled at B. Find the values of p.
The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD . Prove that 2AB2 = 2AC2 + BC2.

In the given figure, ABC is a triangle in which ∠ABC> 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2BC.BD.

Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2(AD2 + CD2)
From the given figure, in ∆ABQ, if AQ = 8 cm, then AB =?

If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

(i) `"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
(ii) `"AB"^2 = "AD"^2 - "BC"."DM" + (("BC")/2)^2`
(iii) `"AC"^2 + "AB"^2 = 2"AD"^2 + 1/2"BC"^2`
In the adjoining figure, a tangent is drawn to a circle of radius 4 cm and centre C, at the point S. Find the length of the tangent ST, if CT = 10 cm.

