Advertisements
Advertisements
प्रश्न
In the adjoining figure, a tangent is drawn to a circle of radius 4 cm and centre C, at the point S. Find the length of the tangent ST, if CT = 10 cm.

विकल्प
`sqrt(21)` cm
`3sqrt(21)` cm
`2sqrt(21)` cm
`4sqrt(21)` cm
उत्तर
`2sqrt(21)` cm
Explanation:
The line from the centre to the tangent is perpendicular to the tangent.
∴ CS ⊥ ST
So, in right angled ΔCST, by the Pythagoras theorem,
CT2 = CS2 + ST2
(10)2 = (4)2 + ST2
ST2 = 100 – 16 = 84
⇒ ST = `2sqrt(21)`
Thus, the length of ST is `2sqrt(21)` cm.
APPEARS IN
संबंधित प्रश्न
If the sides of a triangle are 6 cm, 8 cm and 10 cm, respectively, then determine whether the triangle is a right angle triangle or not.
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
Sides of triangles are given below. Determine it is a right triangles? In case of a right triangle, write the length of its hypotenuse. 3 cm, 8 cm, 6 cm
Digonals of parallelogram WXYZ intersect at point O. If OY =5, find WY.

In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 - `"BD"^2/2`
Find the side of the square whose diagonal is `16sqrt(2)` cm.
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD

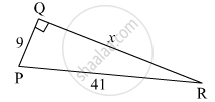
In the figure below, find the value of 'x'.
Two poles of height 9m and 14m stand on a plane ground. If the distance between their 12m, find the distance between their tops.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
AD is perpendicular to the side BC of an equilateral ΔABC. Prove that 4AD2 = 3AB2.
To get from point A to point B you must avoid walking through a pond. You must walk 34 m south and 41 m east. To the nearest meter, how many meters would be saved if it were possible to make a way through the pond?
Choose the correct alternative:
If length of sides of a triangle are a, b, c and a2 + b2 = c2, then which type of triangle it is?
Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is ______.
Two squares having same perimeter are congruent.
Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
