Advertisements
Advertisements
प्रश्न
To get from point A to point B you must avoid walking through a pond. You must walk 34 m south and 41 m east. To the nearest meter, how many meters would be saved if it were possible to make a way through the pond?
उत्तर
In the right ∆ABC,
By Pythagoras theorem
AC2 = AB2 + BC2
= 342 + 412
= 1156 + 1681
= 2837
AC = `sqrt(2837)`
= 53.26 m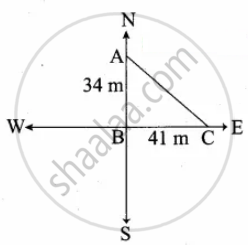
A one must walk (34m + 41m) 75m to reach C.
The difference in Distance = 75 – 53.26
= 21.74 m
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m;
find the distance between their tips.
In equilateral Δ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.
Find the side of the square whose diagonal is `16sqrt(2)` cm.
Triangle ABC is right-angled at vertex A. Calculate the length of BC, if AB = 18 cm and AC = 24 cm.
Find the Pythagorean triplet from among the following set of numbers.
4, 7, 8
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

(i) `"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
(ii) `"AB"^2 = "AD"^2 - "BC"."DM" + (("BC")/2)^2`
(iii) `"AC"^2 + "AB"^2 = 2"AD"^2 + 1/2"BC"^2`
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
If the areas of two circles are the same, they are congruent.
