Advertisements
Advertisements
प्रश्न
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
उत्तर
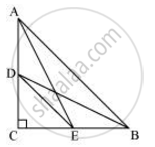
Applying Pythagoras theorem in ΔACE, we obtain
AC2 + CE2 = AE2 ....(i)
Applying Pythagoras theorem in ΔBCD, we get
BC2 + CD2 = BD2 ....(ii)
Using equations (i) and (ii), we get
AC2 + CE2 + BC2 + CD2 = AE2 + BD2 ...(iii)
Applying Pythagoras theorem in ΔCDE, we get
DE2 = CD2 + CE2
Applying Pythagoras theorem in ΔABC, we get
AB2 = AC2 + CB2
Putting these values in equation (iii), we get
DE2 + AB2 = AE2 + BD2.
APPEARS IN
संबंधित प्रश्न
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 − 2BC.BD.

A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
Find the Pythagorean triplet from among the following set of numbers.
2, 4, 5
Find the Pythagorean triplet from among the following set of numbers.
2, 6, 7
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
