Advertisements
Advertisements
प्रश्न
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
उत्तर
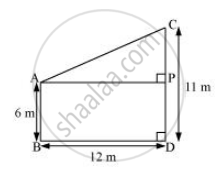
Let CD and AB be the poles of height 11 m and 6 m.
Therefore, CP = 11 − 6 = 5 m
From the figure, it can be observed that AP = 12m
Applying Pythagoras theorem for ΔAPC, we obtain
AP2 + PC2 = AC2
(12 m)2 + (5m)2 = (AC)2
AC2 = (144 + 25)m2 = 169 m2
AC = 13m
Therefore, the distance between their tops is 13 m.
संबंधित प्रश्न
In a ∆ABC, AD ⊥ BC and AD2 = BC × CD. Prove ∆ABC is a right triangle
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
In the given figure, AB//CD, AB = 7 cm, BD = 25 cm and CD = 17 cm;
find the length of side BC.
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 = AD2 + BC x DE + `(1)/(4)"BC"^2`
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?

The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
