Advertisements
Advertisements
प्रश्न
In the given figure, AB//CD, AB = 7 cm, BD = 25 cm and CD = 17 cm;
find the length of side BC.
उत्तर
Take M to be the point on CD such that AB = DM.
So DM = 7cm and MC = 10 cm
Join points B and M to form the line segment BM.
So BM || AD also BM = AD.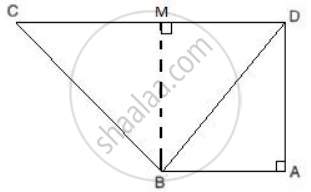
In right-angled ΔBAD,
BD2 = AD2 + BA2
(25)2 = AD2 + (7)2
AD2 = (25)2 - (7)2
AD2 = 576
AD = 24
In right-angled ΔCMB,
CB2 = CM2 + MB2
CB2 = (10)2 + (24)2 ...[ MB = AD ]
CB2 = 100 + 576
CB2 = 676
CB = 26 cm
APPEARS IN
संबंधित प्रश्न
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
Tick the correct answer and justify: In ΔABC, AB = `6sqrt3` cm, AC = 12 cm and BC = 6 cm.
The angle B is:
In the figure: ∠PSQ = 90o, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
In the following Figure ∠ACB= 90° and CD ⊥ AB, prove that CD2 = BD × AD

Show that the triangle ABC is a right-angled triangle; if: AB = 9 cm, BC = 40 cm and AC = 41 cm
Find the Pythagorean triplet from among the following set of numbers.
4, 5, 6
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
AD is perpendicular to the side BC of an equilateral ΔABC. Prove that 4AD2 = 3AB2.
Find the unknown side in the following triangles
In triangle ABC, line I, is a perpendicular bisector of BC.
If BC = 12 cm, SM = 8 cm, find CS
In figure, PQR is a right triangle right angled at Q and QS ⊥ PR. If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
A right-angled triangle may have all sides equal.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
