Advertisements
Advertisements
प्रश्न
M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
उत्तर
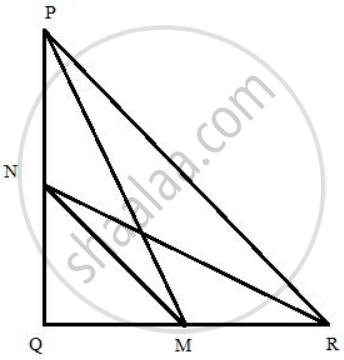
We draw, PM, MN, NR
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Since M and N are the mid-points of the sides QR and PQ respectively, therefore, PN = NQ, QM = RM
(i) First, we consider the ΔPQM, and applying Pythagoras theorem we get,
PM2 = PQ2 + MQ2
= ( PN + NQ )2 + MQ2
= PN + NQ2 + 2PN . NQ + MQ2
= MN2+ PN2 + 2PN.NQ ...[From, ΔMNQ, MN2 = NQ2 + MQ2] ......(i)
Now, we consider the ΔRNQ, and applying Pythagoras theorem we get,
RN2 = NQ2 + RQ2
= NQ2 + ( QM + RM )2
= NQ2 + QM2 + RM2 + 2QM .RM
= MN2 + RM2 + 2QM . RM .......(ii)
Adding (i) and (ii) we get,
PM2 + RN2 = MN2 + PN2 + 2PN.NQ + MN2 + RM2 + 2QM. RM
PM2 + RN2 = 2MN2 + PN2 + RM2 + 2PN.NQ + 2QM.RM
PM2 + RN2 = 2MN2 + NQ2 + QM2 + 2(QN2 ) + 2(QM2 )
PM2 + RN2 = 2MN2 + MN2 + 2MN2
PM2 + RN2 = 5MN2
Hence Proved.
(ii) We consider the ΔPQM, and applying Pythagoras theorem we get,
PM2 = PQ2 + MQ2
4PM2 = 4PQ2 + 4MQ2 ...[ Multiply both sides by 4]
4PM2 = 4PQ2 + 4.`(1/2 "QR")^2` ...[ MQ = `1/2` QR ]
4PM2 = 4PQ2 + 4PQ + 4 . `1/4` QR2
4PM2 = 4PQ2 + QR2
Hence Proved.
(iii) We consider the ΔRQN, and applying Pythagoras theorem we get,
RN2 = NQ2 + RQ2
4RN2 = 4NQ2 + 4QR2 ...[ Multiplying both sides by 4]
4RN2 = 4QR2 + 4 .(1/2 PQ)2 ...[ NQ = `1/2` PQ ]
4RN2 = 4QR2 + 4 .`1/4` PQ2
4RN2 = PQ2 + 4QR2
Hence Proved.
(iv) First, we consider the ΔPQM, and applying Pythagoras theorem we get,
PM2 = PQ2 + MQ2
= ( PN + NQ )2 + MQ2
= PN2 + NQ2 + 2PN.NQ + MQ2
= MN2 + PN2 + 2PN.NQ ...[ From, ΔMNQ, = MN2 = NQ2 + MQ2 ] ......(i)
Now, we consider the ΔRNQ, and applying Pythagoras theorem we get,
RN2 + NQ2 + RQ2
= NQ2 + ( QM + RM )2
= NQ2 + QM2 + RM2 + 2QM .RM
= MN2 + RM2 + 2QM . RM .......(ii)
Adding (i) and (ii) we get,
PM2 + RN2 = MN2 + PN2 + 2PN . NQ + MN2 + RM2 + 2QM. RM
PM2 + RN2 = 2MN2 + PN2 + RM2 + 2PN . NQ + 2QM . RM
PM2 + RN2 = 2MN2 + NQ2 + QM2 + 2(QN2 ) + 2(QM2 )
PM2 + RN2 = 2MN2 + MN2 + 2MN2
PM 2 + RN2 = 5MN2
4( PM2 + RN2 ) = 4.5. (NQ2 + MQ2)
4( PM2 + RN2 ) = 4.5. `[ ( 1/2 "PQ" )^2 + ( 1/2 "RQ" )^2 ] ....[ ∵ "NQ" = 1/2 "PQ" , "MQ" = 1/2 "QR" ]`
4 ( PM2 + RN2 ) = 5PR2
Hence Proved.
APPEARS IN
संबंधित प्रश्न
Side of a triangle is given, determine it is a right triangle.
`(2a – 1) cm, 2\sqrt { 2a } cm, and (2a + 1) cm`
ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that
(i) cp = ab
`(ii) 1/p^2=1/a^2+1/b^2`
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD

Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
In the following figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that

(i) OA2 + OB2 + OC2 − OD2 − OE2 − OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
For finding AB and BC with the help of information given in the figure, complete following activity.
AB = BC .......... 
∴ ∠BAC = 
∴ AB = BC =  × AC
× AC
=  × `sqrt8`
× `sqrt8`
=  × `2sqrt2`
× `2sqrt2`
= 

In the given figure, AB//CD, AB = 7 cm, BD = 25 cm and CD = 17 cm;
find the length of side BC.
In triangle ABC, AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2.
Find x.
In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
In an isosceles triangle ABC; AB = AC and D is the point on BC produced.
Prove that: AD2 = AC2 + BD.CD.
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
Prove that in a right angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

Find the Pythagorean triplet from among the following set of numbers.
2, 6, 7
A ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
Two poles of height 9m and 14m stand on a plane ground. If the distance between their 12m, find the distance between their tops.
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?

