Advertisements
Advertisements
प्रश्न
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
उत्तर
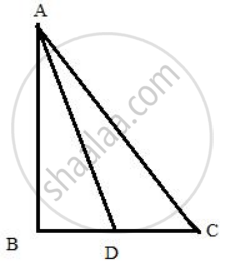
In ΔABC
AB2 + BC2 = AC2
as [BC = 2CD]
AB2 + 4CD2 = AC2 ....(1)
In ΔABD,
AD2 = AB2 + BD2 = AB2 + CD2 ....(2)
Subtracting (1) and (2)
AC2 - AD2 = AB2 + 4CD2 - (AB2 + CD2)
AC2 - AD2 = 3CD2
AC2 = AD2 + 3CD2
Hence proved.
APPEARS IN
संबंधित प्रश्न
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD

In Figure ABD is a triangle right angled at A and AC ⊥ BD. Show that AC2 = BC × DC

Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
Choose the correct alternative:
In right-angled triangle PQR, if hypotenuse PR = 12 and PQ = 6, then what is the measure of ∠P?
Show that the triangle ABC is a right-angled triangle; if: AB = 9 cm, BC = 40 cm and AC = 41 cm
In the figure below, find the value of 'x'.

From the given figure, find the length of hypotenuse AC and the perimeter of ∆ABC.
A man goes 10 m due east and then 24 m due north. Find the distance from the straight point.
A point OI in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D. Prove that OB2 + OD2 = OC2 + OA2
Find the unknown side in the following triangles
Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is ______.

A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
In the adjoining figure, a tangent is drawn to a circle of radius 4 cm and centre C, at the point S. Find the length of the tangent ST, if CT = 10 cm.

Two angles are said to be ______, if they have equal measures.
Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

