Advertisements
Advertisements
Question
To get from point A to point B you must avoid walking through a pond. You must walk 34 m south and 41 m east. To the nearest meter, how many meters would be saved if it were possible to make a way through the pond?
Solution
In the right ∆ABC,
By Pythagoras theorem
AC2 = AB2 + BC2
= 342 + 412
= 1156 + 1681
= 2837
AC = `sqrt(2837)`
= 53.26 m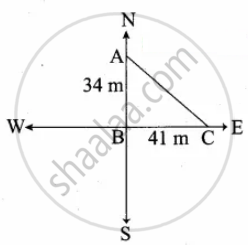
A one must walk (34m + 41m) 75m to reach C.
The difference in Distance = 75 – 53.26
= 21.74 m
APPEARS IN
RELATED QUESTIONS
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.
The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD . Prove that 2AB2 = 2AC2 + BC2.

Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)
In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF

In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

The given figure shows a quadrilateral ABCD in which AD = 13 cm, DC = 12 cm, BC = 3 cm and ∠ABD = ∠BCD = 90o. Calculate the length of AB.
Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 - `"BD"^2/2`
In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

Use the information given in the figure to find the length AD.

Find the Pythagorean triplet from among the following set of numbers.
4, 7, 8
