Advertisements
Advertisements
Question
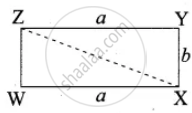
In the rectangle WXYZ, XY + YZ = 17 cm, and XZ + YW = 26 cm. Calculate the length and breadth of the rectangle?
Advertisements
Solution
Let the length of the rectangle be “a” and the breadth of the rectangle be “b”.
XY + YZ = 17 cm
b + a = 17 ...(1)
In the right ∆WXZ,
XZ2 = WX2 + WZ2
(XZ)2 = a2 + b2
XZ = `sqrt("a"^2 + "b"^2)`
Similarly WY = `sqrt("a"^2 + "b"^2)`
⇒ XZ + WY = 26
⇒ `2sqrt("a"^2 + "b"^2)` = 26
⇒ `sqrt("a"^2 + "b"^2)` = 13
Squaring on both sides
a2 + b2 = 169
(a + b)2 – 2ab = 169
172 – 2ab = 169
⇒ 289 – 169 = 2ab
⇒ 120 = 2ab
⇒ ab = 60
a = `60/"b"` ...(2)
Substituting the value of a = `60/"b"` in (1)
`60/"b" +"b"` = 17
b2 – 17b + 60 = 0
(b – 2) (b – 5) = 0
b = 12 or b = 5
If b = 12
⇒ a = 5
If b = 6
⇒ a = 12
Length = 12 m and breadth = 5 m
APPEARS IN
RELATED QUESTIONS
In ∆PQR, PQ = √8 , QR = √5 , PR = √3. Is ∆PQR a right-angled triangle? If yes, which angle is of 90°?
Sides of the triangle are 7 cm, 24 cm, and 25 cm. Determine whether the triangle is a right-angled triangle or not.
The hypotenuse of a right triangle is 6 m more than twice of the shortest side. If the third side is 2 m less than the hypotenuse, find the sides of the triangle
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
12, 13, 15
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
9, 40, 41
The area of a rectangle of length 21 cm and diagonal 29 cm is __________
A rectangle having length of a side is 12 and length of diagonal is 20, then what is length of other side?
In ∆ABC, AB = `6sqrt(3)` cm, AC = 12 cm, and BC = 6 cm then m∠A = ?
If a triangle having sides 50 cm, 14 cm and 48 cm, then state whether given triangle is right angled triangle or not
In ∆LMN, l = 5, m = 13, n = 12 then complete the activity to show that whether the given triangle is right angled triangle or not.
*(l, m, n are opposite sides of ∠L, ∠M, ∠N respectively)
Activity: In ∆LMN, l = 5, m = 13, n = `square`
∴ l2 = `square`, m2 = 169, n2 = 144.
∴ l2 + n2 = 25 + 144 = `square`
∴ `square` + l2 = m2
∴ By Converse of Pythagoras theorem, ∆LMN is right angled triangle.
