Advertisements
Advertisements
Question
The hypotenuse of a right triangle is 6 m more than twice of the shortest side. If the third side is 2 m less than the hypotenuse, find the sides of the triangle
Solution
Let the shortest side of the right triangle be x.
∴ Hypotenuse = 6 + 2x
Third side = 2x + 6 – 2
= 2x + 4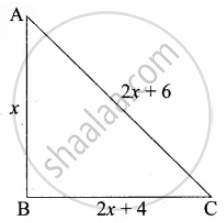
In the right triangle ABC,
AC2 = AB2 + BC2
(2x + 6)2 = x2 + (2x + 4)2
4x2 + 36 + 24x = x2 + 4x2 + 16 + 16x
0 = x2 – 24x + 16x – 36 + 16
∴ x2 – 8x – 20 = 0
(x – 10) (x + 2) = 0
x – 10 = 0 or x + 2 = 0
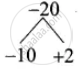
x = 10 or x = – 2 ...(Negative value will be omitted)
The side AB = 10 m
The side BC = 2(10) + 4 = 24 m
Hypotenuse AC = 2(10) + 6 = 26 m
APPEARS IN
RELATED QUESTIONS
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. The length of the side AC is
If the sides of a triangle are in the ratio 5 : 12 : 13 then, it is ________
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
12, 13, 15
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
24, 45, 51
Choose the correct alternative:
A rectangle having length of a side is 12 and length of diagonal is 20, then what is length of other side?
If a triangle having sides 8 cm, 15 cm and 17 cm, then state whether given triangle is right angled triangle or not
A rectangle having dimensions 35 m × 12 m, then what is the length of its diagonal?
In ∆LMN, l = 5, m = 13, n = 12 then complete the activity to show that whether the given triangle is right angled triangle or not.
*(l, m, n are opposite sides of ∠L, ∠M, ∠N respectively)
Activity: In ∆LMN, l = 5, m = 13, n = `square`
∴ l2 = `square`, m2 = 169, n2 = 144.
∴ l2 + n2 = 25 + 144 = `square`
∴ `square` + l2 = m2
∴By Converse of Pythagoras theorem, ∆LMN is right angled triangle.
In ΔABC, AB = 9 cm, BC = 40 cm, AC = 41 cm. State whether ΔABC is a right-angled triangle or not. Write reason.
In a right angled triangle, right-angled at B, lengths of sides AB and AC are 5 cm and 13 cm, respectively. What will be the length of side BC?
