Advertisements
Advertisements
Question
5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
Solution
“C” is the position of the foot of the ladder “A” is the position of the top of the ladder.
In the right ∆ABC,
BC2 = AC2 – AB2
= 52 – 42
= 25 – 16
= 9
BC = `sqrt(9)` = 3 m
When the foot of the ladder moved 1.6 m toward the wall.
The distance between the foot of the ladder to the ground is
BE = 3 – 1.6 m = 1.4 m
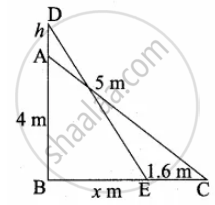
Let the distance moved upward on the wall be “h” m
The ladder touch the wall at (4 + h) M
In the right ∆BED,
ED2 = AB2 + BE2
52 = (4 + h)2 + (1.4)2
25 – 1.96 = (4 + h)2
∴ 4 + h = `sqrt(23.04)`
4 + h = 4.8 m
h = 4.8 – 4
= 0.8 m
Distance moved upward on the wall = 0.8 m
APPEARS IN
RELATED QUESTIONS
Sides of the triangle are 7 cm, 24 cm, and 25 cm. Determine whether the triangle is a right-angled triangle or not.
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
12, 13, 15
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
9, 40, 41
The area of a rectangle of length 21 cm and diagonal 29 cm is __________
Choose the correct alternative:
A rectangle having length of a side is 12 and length of diagonal is 20, then what is length of other side?
Choose the correct alternative:
If length of both diagonals of rhombus are 60 and 80, then what is the length of side?
If a triangle having sides 50 cm, 14 cm and 48 cm, then state whether given triangle is right angled triangle or not
A rectangle having dimensions 35 m × 12 m, then what is the length of its diagonal?
In ∆LMN, l = 5, m = 13, n = 12 then complete the activity to show that whether the given triangle is right angled triangle or not.
*(l, m, n are opposite sides of ∠L, ∠M, ∠N respectively)
Activity: In ∆LMN, l = 5, m = 13, n = `square`
∴ l2 = `square`, m2 = 169, n2 = 144.
∴ l2 + n2 = 25 + 144 = `square`
∴ `square` + l2 = m2
∴By Converse of Pythagoras theorem, ∆LMN is right angled triangle.
In the given figure, triangle PQR is right-angled at Q. S is the mid-point of side QR. Prove that QR2 = 4(PS2 – PQ2).

