Advertisements
Advertisements
Question
The area of a rectangle of length 21 cm and diagonal 29 cm is __________
Options
609 cm2
580 cm2
420 cm2
210 cm2
Solution
420 cm2
Explanation;
Hint: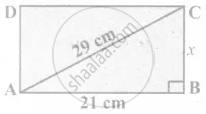
length = 21 cm
diagonal = 29 cm
By the converse of Pythagoras theorem,
AB2 + BC2 = AC2
212 + x2 = 292
x2 = 841 – 441
400 = 202
x = 20 cm
Now area of the rectangle = length × breadth.
i.e AB × BC
= 21 cm × 20 cm
= 420 cm2
APPEARS IN
RELATED QUESTIONS
5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
If in ∆ABC, DE || BC. AB = 3.6 cm, AC = 2.4 cm and AD = 2.1 cm then the length of AE is
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m, what is the distance between their tops?
The incentre is equidistant from all the vertices of a triangle
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
12, 13, 15
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
30, 40, 50
Choose the correct alternative:
In right angled triangle, if sum of the squares of the sides of right angle is 169, then what is the length of the hypotenuse?
Choose the correct alternative:
If the length of diagonal of square is √2, then what is the length of each side?
Choose the correct alternative:
In ∆ABC, AB = `6sqrt(3)` cm, AC = 12 cm, and BC = 6 cm, then m∠A = ?
In a right angled triangle, right-angled at B, lengths of sides AB and AC are 5 cm and 13 cm, respectively. What will be the length of side BC?
