Advertisements
Advertisements
प्रश्न
The hypotenuse of a right triangle is 6 m more than twice of the shortest side. If the third side is 2 m less than the hypotenuse, find the sides of the triangle
Advertisements
उत्तर
Let the shortest side of the right triangle be x.
∴ Hypotenuse = 6 + 2x
Third side = 2x + 6 – 2
= 2x + 4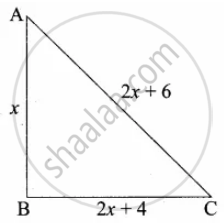
In the right triangle ABC,
AC2 = AB2 + BC2
(2x + 6)2 = x2 + (2x + 4)2
4x2 + 36 + 24x = x2 + 4x2 + 16 + 16x
0 = x2 – 24x + 16x – 36 + 16
∴ x2 – 8x – 20 = 0
(x – 10) (x + 2) = 0
x – 10 = 0 or x + 2 = 0
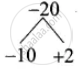
x = 10 or x = – 2 ...(Negative value will be omitted)
The side AB = 10 m
The side BC = 2(10) + 4 = 24 m
Hypotenuse AC = 2(10) + 6 = 26 m
APPEARS IN
संबंधित प्रश्न
5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
In the adjacent figure, ABC is a right angled triangle with right angle at B and points D, E trisect BC. Prove that 8AE2 = 3AC2 + 5AD2
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. The length of the side AC is
The incentre is equidistant from all the vertices of a triangle
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
8, 15, 17
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
9, 40, 41
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
24, 45, 51
Choose the correct alternative:
In ∆ABC, AB = `6sqrt(3)` cm, AC = 12 cm, and BC = 6 cm, then m∠A = ?
A rectangle having dimensions 35 m × 12 m, then what is the length of its diagonal?
In ΔABC, AB = 9 cm, BC = 40 cm, AC = 41 cm. State whether ΔABC is a right-angled triangle or not. Write reason.
