Advertisements
Advertisements
प्रश्न
If in ∆ABC, DE || BC. AB = 3.6 cm, AC = 2.4 cm and AD = 2.1 cm then the length of AE is
विकल्प
1.4 cm
1.8 cm
1.2 cm
1.05 cm
उत्तर
1.4 cm
Explanation;
Hint: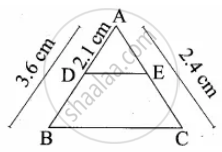
In ∆ABC and ADE
`"AB"/"AD" = "AC"/"AE" ⇒ 3.6/2.1 = 2.4/"AE"`
3.6 × AE = 2.4 × 2.1
AE = `(2.4 xx 2.1)/3.6 = (24 xx 21)/360`
AE = 1.4 cm
APPEARS IN
संबंधित प्रश्न
In ∆PQR, PQ = √8 , QR = √5 , PR = √3. Is ∆PQR a right-angled triangle? If yes, which angle is of 90°?
Sides of the triangle are 7 cm, 24 cm, and 25 cm. Determine whether the triangle is a right-angled triangle or not.
5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m, what is the distance between their tops?
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
30, 40, 50
The area of a rectangle of length 21 cm and diagonal 29 cm is __________
Choose the correct alternative:
If the length of diagonal of square is √2, then what is the length of each side?
A rectangle having dimensions 35 m × 12 m, then what is the length of its diagonal?
In ∆LMN, l = 5, m = 13, n = 12 then complete the activity to show that whether the given triangle is right angled triangle or not.
*(l, m, n are opposite sides of ∠L, ∠M, ∠N respectively)
Activity: In ∆LMN, l = 5, m = 13, n = `square`
∴ l2 = `square`, m2 = 169, n2 = 144.
∴ l2 + n2 = 25 + 144 = `square`
∴ `square` + l2 = m2
∴By Converse of Pythagoras theorem, ∆LMN is right angled triangle.
In ΔABC, AB = 9 cm, BC = 40 cm, AC = 41 cm. State whether ΔABC is a right-angled triangle or not. Write reason.
