Advertisements
Advertisements
प्रश्न
The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is
विकल्प
`6 2/3` cm
`(10sqrt(6))/3` cm
`66 2/3` cm
15 cm
उत्तर
15 cm
Explanation;
Hint:
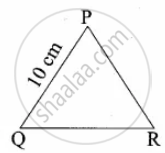
`("Perimeter of" Delta "ABC")/("Perimeter of" Delta "PQR") = "AB"/"PQ"`
`36/24 = "AB"/10`
36 × 10 = 24 AB
AB = `(36 xx 10)/24`
AB = 15 cm
APPEARS IN
संबंधित प्रश्न
The two similar triangles are equal in area. Prove that the triangles are congruent.
In the given figure, ∠ABC = 90° and BD⊥AC. If AB = 5.7cm, BD = 3.8cm and CD = 5.4cm, find BC.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 8cm, AB = 12cm and AE = 12cm, find CE.
Prove that the external bisector of an angle of a triangle divides the opposite side externally n the ratio of the sides containing the angle.
Find the scale factor in each of the following and state the type of size transformation:
Model volume = 200cm3, Actual volume = 8cm3
If BD ⊥ AC and CE ⊥ AB, prove that ∆AEC ~ ∆ADB

A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
In the given figure, if ΔEAT ~ ΔBUN, find the measure of all angles.
It is given that ΔABC ~ ΔPQR, with `(BC)/(QR) = 1/3`. Then, `(ar(PRQ))/(ar(BCA))` is equal to ______.
In figure, if AD = 6cm, DB = 9cm, AE = 8cm and EC = 12cm and ∠ADE = 48°. Find ∠ABC.

