Advertisements
Advertisements
प्रश्न
Prove that the external bisector of an angle of a triangle divides the opposite side externally n the ratio of the sides containing the angle.
उत्तर
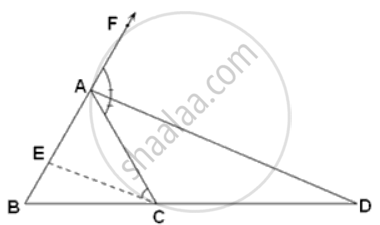
In ΔABC, CE || AD
∴ `"BD"/"CD" = "AB"/"AE"`.....(i)
(By Basic Proportionality theorem)
AD is e bisector of ∠CAF
∠FAD = ∠CAD......(ii)
Since CE || AD
Therefore,
∠ACE = ∠CAD......(iii) ...(alternate angles)
∠AEC = ∠FAD......(iv) ...(corresponding angles)
From (ii) and (iii) and (iv)
∠AEC = ∠ACE
In ΔAEC,
∠AEC = ∠ACE
AC = AE ......(v) ...(Equal angles have equal sides opposite to them)
From (i) and (v)
`"BD"/"CD" = "AB"/"AC"`.
APPEARS IN
संबंधित प्रश्न
In the given figure ΔABC and ΔAMP are right angled at B and M respectively. Given AC = 10 cm, AP = 15 cm and PM = 12 cm.

1) Prove ΔABC ~ ΔAMP
2) Find AB and BC.
ΔABC~ΔDEF and their areas are respectively 64 cm2 and 121cm2. If EF = 15.4cm, find BC.
ΔABC is right angled at A and AD⊥BC. If BC = 13cm and AC = 5cm, find the ratio of the areas of ΔABC and ΔADC.
State the SAS-similarity criterion
Δ ABC ∼ Δ PQR. AD and PS are altitudes from A and P on sides BC and QR respectively. If AD : PS = 4 : 9 , find the ratio of the areas of Δ ABC and Δ PQR.
In figure , DEF is a right -angled triangle with ∠ E = 90 °.FE is produced to G and GH is drawn perpendicular to DE = 8 cm , DH = 8 cm ,DH = 6 cm and HF = 4 cm , find `("Ar" triangle "DEF")/("Ar" triangle "GHF")`

In the figure, AB || RQ and BC || SQ, prove that `"PC"/"PS" = "PA"/"PR"`.
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate:Length of B' C', if BC = 8cm
A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
State whether the following triangles are similar or not: If yes, then write the test of similarity.
∠P = 35°, ∠X = 35° and ∠Q = 60°, ∠Y = 60°

