Advertisements
Advertisements
प्रश्न
Δ ABC ∼ Δ PQR. AD and PS are altitudes from A and P on sides BC and QR respectively. If AD : PS = 4 : 9 , find the ratio of the areas of Δ ABC and Δ PQR.
उत्तर
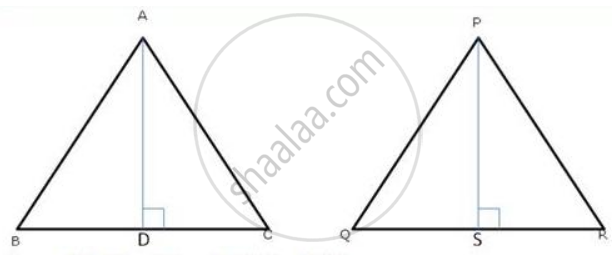
Given : AD : PS = 4 : 9 and Δ ABC ∼ Δ PQR
To Find : `("Ar" triangle "ABC")/("Ar" triangle "PQR")`
Sol : `("Ar" triangle "ABC")/("Ar" triangle "PQR") = ("AB"^2)/("PQ"^2)` .......(1)
[The ratio of area of two similar triangles is equal to the ratio of square of their corresponding sides]
In Δ BAD and Δ QPS
∠ B = ∠ Q (Δ ABC ∼ Δ PQR)
∠AOB = ∠PSQ (90° each)
Δ BAD ∼ Δ QPS (AA corollary)
`therefore "AB"/"PQ" = "AD"/"PS"` ........(2) (similar sides of similar triangles)
Using (1) and (2)
`("Ar" triangle "ABC")/("Ar" triangle "PQR") = "AD"^2/"PS"^2 = (4/9)^2 = 16/81`
Required ratio is 16 : 81.
APPEARS IN
संबंधित प्रश्न
In figure, ∠CAB = 90º and AD ⊥ BC. If AC = 75 cm, AB = 1 m and BD = 1.25 m, find AD.
In triangle ABC, AD is perpendicular to side BC and AD2 = BD × DC. Show that angle BAC = 90°.
In the figure, parts of the two triangles bearing identical marks are
congruent. State the test by which the triangles are congruent.

In Δ ABC , MN || BC .

If BC = 14 cm and MN = 6 cm , find `("Ar" triangle "AMN")/("Ar" . ("trapezium MBCN"))`
A model of a ship is made to a scale 1 : 300.
- The length of the model of the ship is 2 m. Calculate the length of the ship.
- The area of the deck of the ship is 180,000 m2. Calculate the area of the deck of the model.
- The volume of the model is 6.5 m3. Calculate the volume of the ship.
Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are `3/5` of the corresponding sides of the first triangle.
ΔABC is right angled at A. AD is drawn perpendicular to BC. If AB = 8cm and AC = 6cm, calculate BD.
A map is drawn to scale of 1:20000. Find: The distance on the map representing 4km
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The base area of the truck, if the base area of the model is 30m2
In the figure, if ∠FEG ≡ ∠1 then, prove that DG2 = DE.DF
