Advertisements
Advertisements
Question
Δ ABC ∼ Δ PQR. AD and PS are altitudes from A and P on sides BC and QR respectively. If AD : PS = 4 : 9 , find the ratio of the areas of Δ ABC and Δ PQR.
Solution
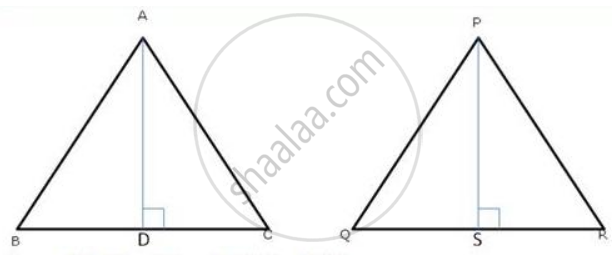
Given : AD : PS = 4 : 9 and Δ ABC ∼ Δ PQR
To Find : `("Ar" triangle "ABC")/("Ar" triangle "PQR")`
Sol : `("Ar" triangle "ABC")/("Ar" triangle "PQR") = ("AB"^2)/("PQ"^2)` .......(1)
[The ratio of area of two similar triangles is equal to the ratio of square of their corresponding sides]
In Δ BAD and Δ QPS
∠ B = ∠ Q (Δ ABC ∼ Δ PQR)
∠AOB = ∠PSQ (90° each)
Δ BAD ∼ Δ QPS (AA corollary)
`therefore "AB"/"PQ" = "AD"/"PS"` ........(2) (similar sides of similar triangles)
Using (1) and (2)
`("Ar" triangle "ABC")/("Ar" triangle "PQR") = "AD"^2/"PS"^2 = (4/9)^2 = 16/81`
Required ratio is 16 : 81.
APPEARS IN
RELATED QUESTIONS
In the following figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
In figure, PQ is parallel to BC, AP : AB = 2 : 7. If QC = 0 and BC = 21,
Find
(i) AQ
(ii) PQ
In the figure, DE || AC and DC || AP. Prove that `"BE"/"EC" = "BC"/"CP"`
On a map drawn to a scale of 1: 2,50,000, a triangular plot of land has the following measurements:
AB = 3 cm, BC = 4 cm, ∠ABC = 90°. Calculate:
(i) The actual length of AB in km.
(ii) The area of Plot in sq. km.
A model of a ship is made to a scale of 1:500. Find: The volume of the model when the volume of the ship is 1km3
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆QMO ~ ∆RPN

In Quadrilateral ABCD, side AD || BC, diagonal AC and BD intersect in point P, then prove that `"AP"/"PD" = "PC"/"BP"`
In figure, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.
In figure, if AD = 6 cm, DB = 9 cm, AE = 8 cm and EC = 12 cm and ∠ADE = 48°. Find ∠ABC.

