Advertisements
Advertisements
Question
Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
Solution
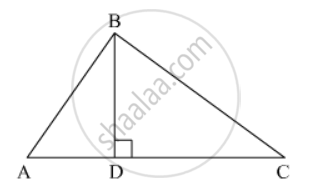
Given: A right ΔABC right angled at B
To prove : AC2 = AB2 + BC2
Construction: Draw AD ⊥ AC
Proof: ΔADB and ΔABC
∠ADB = ∠ABC = 90°
∠BAD = ∠BAC (common)
∴ ΔADB ∼ ΔABC (by AA similarly criterion)
`=> (AD)/(AB) = (AB)/(AC)`
⇒ AD × AC = AB2 ...... (1)
Now In ΔBDC and ΔABC
∠BDC = ∠ABC = 90°
∠BCD = ∠BCA (common)
∴ ΔBDC ∼ ΔABC (by AA similarly criterion)
`=> (CD)/(BC) = (BC)/(AC)`
⇒ CD × AC = BC2 ........ (2)
Adding (1) and (2) we get
AB2 + BC2 = AD × AC + CD × AC
= AC (AD + CD)
= AC × AC = AC2
∴ AC2 = AB2 + BC2
Hence Proved.
APPEARS IN
RELATED QUESTIONS
If a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side of the perpendicular are similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse
Prove that the line segments joining the mid points of the sides of a triangle form four triangles, each of which is similar to the original triangle
In the given figure, AB and DE are perpendicular to BC.

1) Prove that ΔABC ∼ ΔDEC
2) If AB = 6 cm; DE = 4 cm and AC = 15 cm. Calculate CD.
3) Find the ratio of area of ΔABC: area of ΔDEC
In triangle ABC, DE is parallel to BC; where D and E are the points on AB and AC respectively.
Prove: ∆ADE ~ ∆ABC.
Also, find the length of DE, if AD = 12 cm, BD = 24 cm BC = 8 cm.
Given: FB = FD, AE ⊥ FD and FC ⊥ AD.
Prove that: `(FB)/(AD) = (BC)/(ED)`.

P and Q are points on the sides AB and AC respectively of a ΔABC. If AP = 2cm, PB = 4cm, AQ = 3cm and QC = 6cm, show that BC = 3PQ.
In an isosceles ΔABC, the base AB is produced both ways in P and Q such that
AP × BQ = AC2.
Prove that ΔACP~ΔBCQ.

In a right triangle ABC, right angled at B, D is a point on hypotenuse such that BD ⊥ AC , if DP ⊥ AB and DQ ⊥ BC then prove that
`(a) DQ^2 Dp.QC (b) DP ^2 DQ.AP 2 `

In Figure 3, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and DC is 14 cm. If arcs of equal radii 7 cm have been drawn, with centres A,B, C and D, then find the area of the shaded region.

In Δ ABC , DE is parallel to BC and `"AD"/"DB" = 2/7` IF AC = 5 .6 , find AE.
In figure , DEF is a right -angled triangle with ∠ E = 90 °.FE is produced to G and GH is drawn perpendicular to DE = 8 cm , DH = 8 cm ,DH = 6 cm and HF = 4 cm , find `("Ar" triangle "DEF")/("Ar" triangle "GHF")`

D and E are points on the sides AB and AC respectively of Δ ABC such that AB=5.6cm, AD= 1.4cm, AC=7 .2cm and AE = 1.5 cm, show that DE is parallel to BC
A model of a ship is made with a scale factor of 1 : 500. Find
The length of the ship, if the model length is 60 cm.
In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find :
- `(CP)/(PA)`
- PQ
- If AP = x, then the value of AC in terms of x.

In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if:
- AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm.
- AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
Sides of a triangle are 7, 24 and 25. Determine whether the triangle is a right-angled triangle or not.
Find the area of the triangle ABC with the coordinates of A as (1, −4) and the coordinates of the mid-points of sides AB and AC respectively are (2, −1) and (0, −1).
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AD"/"AB"`
In ΔABC, point D divides AB in the ratio 5:7, Find: DE, If BC = 4.8cm
In a triangle ABC, AB = 4 cm, BC = 4.5 cm and CA = 5 cm. Construct ΔABC. Find the image A'B'C of the ΔABC obtained by enlarging it by a scale factor 2. Measure the sides of the image A'B'C' and show that AB:A'B' = AC:B'C' = CA:C'A'
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆QMO ~ ∆RPN

Construct a triangle similar to a given triangle LMN with its sides equal to `4/5` of the corresponding sides of the triangle LMN (scale factor `4/5 < 1`)
In the given figure AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y cm. Find x and y.
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 + c2 = `2"p"^2 + "a"^2/2`
In the given figure, if ΔEAT ~ ΔBUN, find the measure of all angles.
Two similar triangles will always have ________ angles
Which of the following is not a test of similarity?
ΔABC ~ ΔDEF. Write the ratios of their corresponding sides
In ΔABC, AP ⊥ BC and BQ ⊥ AC, B−P−C, A−Q−C, then show that ΔCPA ~ ΔCQB. If AP = 7, BQ = 8, BC = 12, then AC = ?

In ΔCPA and ΔCQB
∠CPA ≅ [∠ ______] ...[each 90°]
∠ACP ≅ [∠ ______] ...[common angle]
ΔCPA ~ ΔCQB ......[______ similarity test]
`"AP"/"BQ" = (["______"])/"BC"` .......[corresponding sides of similar triangles]
`7/8 = (["______"])/12`
AC × [______] = 7 × 12
AC = 10.5
The ratio of the corresponding altitudes of two similar triangles is `3/5`. Is it correct to say that ratio of their areas is `6/5`? Why?
