Advertisements
Advertisements
प्रश्न
Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
उत्तर
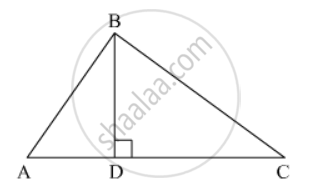
Given: A right ΔABC right angled at B
To prove : AC2 = AB2 + BC2
Construction: Draw AD ⊥ AC
Proof: ΔADB and ΔABC
∠ADB = ∠ABC = 90°
∠BAD = ∠BAC (common)
∴ ΔADB ∼ ΔABC (by AA similarly criterion)
`=> (AD)/(AB) = (AB)/(AC)`
⇒ AD × AC = AB2 ...... (1)
Now In ΔBDC and ΔABC
∠BDC = ∠ABC = 90°
∠BCD = ∠BCA (common)
∴ ΔBDC ∼ ΔABC (by AA similarly criterion)
`=> (CD)/(BC) = (BC)/(AC)`
⇒ CD × AC = BC2 ........ (2)
Adding (1) and (2) we get
AB2 + BC2 = AD × AC + CD × AC
= AC (AD + CD)
= AC × AC = AC2
∴ AC2 = AB2 + BC2
Hence Proved.
APPEARS IN
संबंधित प्रश्न
In the figure given below, Ray PT is bisector of ∠QPR. If PQ = 5.6 cm, QT = 4 cm and TR = 5 cm, find the value of x .

E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR:
PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that `("AO")/("BO") = ("CO")/("DO")`
Given: ∠GHE = ∠DFE = 90°,
DH = 8, DF = 12,
DG = 3x – 1 and DE = 4x + 2.

Find: the lengths of segments DG and DE.
In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N.

Find the lengths of PN and RM.
The perimeter of two similar triangles are 30 cm and 24 cm. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
In the given figure, ∠ABC = 90° and BD⊥AC. If BD = 8cm, AD = 4cm, find CD.
In the given figure, seg XY || seg BC, then which of the following statements is true?

In the figure, parts of the two triangles bearing identical marks are
congruent. State the test by which the triangles are congruent.

In ΔPQR, PQ = 10 cm, QR = 12cm, PR = 8 cm, find the biggest and the smallest angle of the triangle.
Δ ABC ∼ Δ PQR. AD and PS are altitudes from A and P on sides BC and QR respectively. If AD : PS = 4 : 9 , find the ratio of the areas of Δ ABC and Δ PQR.
A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate : the length of C' A' if CA = 4 cm.
In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find :
- `(CP)/(PA)`
- PQ
- If AP = x, then the value of AC in terms of x.

The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.

In fig.DE || BC ,AD = 1 cm and BD = 2 cm. what is the ratio of the ar(ΔABC) to the ar (ΔADE)?

In the adjoining figure, the medians BD and CE of a ∆ABC meet at G. Prove that
(i) ∆EGD ∼ ∆CGB and
(ii) BG = 2GD for (i) above.
In the given figure, PB is the bisector of ABC and ABC =ACB. Prove that:
a. BC x AP = PC x AB
b. AB:AC = BP: BC
A plot of land of area 20km2 is represented on the map with a scale factor of 1:200000. Find: The ground area in km2 that is represented by 2cm2 on the map.
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The volume of the model if the volume of the truck is 6m3
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The diagonal distance of the plot in km
Check whether the triangles are similar and find the value of x
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆RPN

Construct a triangle similar to a given triangle LMN with its sides equal to `4/5` of the corresponding sides of the triangle LMN (scale factor `4/5 < 1`)
Construct a triangle similar to a given triangle PQR with its sides equal to `7/3` of the corresponding sides of the triangle PQR (scale factor `7/3 > 1`)
If in triangles ABC and EDF, `"AB"/"DE" = "BC"/"FD"` then they will be similar, when
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 + c2 = `2"p"^2 + "a"^2/2`
Given ΔABC ~ ΔDEF, if ∠A = 45° and ∠E = 35° then ∠B = ?
Write the test of similarity for triangles given in figure.
