Advertisements
Advertisements
प्रश्न
In the adjoining figure, the medians BD and CE of a ∆ABC meet at G. Prove that
(i) ∆EGD ∼ ∆CGB and
(ii) BG = 2GD for (i) above.
उत्तर
Since D and E are mid-point of AC and AB respectively in ∆ABC, Ed is parallel to BC.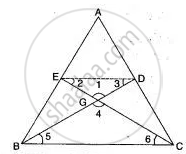
(i) In ∆'s EGD and CGB,
∠EGD = ∠CGB ...(Vertically opp., angles)
∠EGD = ∠CBG ...(Alternative angles)
So, ∆EGD ∼ ∆CGB.
Hence proved.
(ii) ∴ `"BG"/"GD" = "BC"/"DE"`
But `"BC"/"DE" = 2, "So" "BG"/"GD" = 2`
⇒ BG = 2GD.
Hence Proved.
APPEARS IN
संबंधित प्रश्न
In figure, ∠CAB = 90º and AD ⊥ BC. If AC = 75 cm, AB = 1 m and BD = 1.25 m, find AD.
In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N.

Find the lengths of PN and RM.
The corresponding sides of two similar triangles ABC and DEF are BC = 9.1cm and EF = 6.5cm. If the perimeter of ΔDEF is 25cm, find the perimeter of ΔABC.
State the SSS-similarity criterion for similarity of triangles
Δ ABC ~ Δ DEF. If BC = 3cm , EF=4cm and area of Δ ABC = 54 cm2 , find area of Δ DEF.
In Δ ABC , MN || BC .

If BC = 14 cm and MN = 6 cm , find `("Ar" triangle "AMN")/("Ar" . ("trapezium MBCN"))`
D and E are points on the sides AB and AC respectively of Δ ABC such that AB=5.6cm, AD= 1.4cm, AC=7 .2cm and AE = 1.5 cm, show that DE is parallel to BC
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 11, SQ = 12, PR = 22. Find QR.

In the following figure, point D divides AB in the ratio 3 : 5. Find :
BC = 4.8 cm, find the length of DE.

If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆QMO

