Advertisements
Advertisements
Question
In the adjoining figure, the medians BD and CE of a ∆ABC meet at G. Prove that
(i) ∆EGD ∼ ∆CGB and
(ii) BG = 2GD for (i) above.
Solution
Since D and E are mid-point of AC and AB respectively in ∆ABC, Ed is parallel to BC.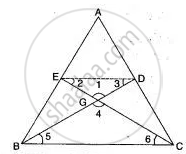
(i) In ∆'s EGD and CGB,
∠EGD = ∠CGB ...(Vertically opp., angles)
∠EGD = ∠CBG ...(Alternative angles)
So, ∆EGD ∼ ∆CGB.
Hence proved.
(ii) ∴ `"BG"/"GD" = "BC"/"DE"`
But `"BC"/"DE" = 2, "So" "BG"/"GD" = 2`
⇒ BG = 2GD.
Hence Proved.
APPEARS IN
RELATED QUESTIONS
The perimeters of two similar triangles ABC and PQR are respectively 36 cm and 24 cm. If PQ = 10 cm, find AB
In figure, ∠CAB = 90º and AD ⊥ BC. If AC = 75 cm, AB = 1 m and BD = 1.25 m, find AD.
In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC ∼ ΔPDB
(ii) PA.PB = PC.PD

The corresponding altitudes of two similar triangles are 6cm and 9cm respectively. Find the ratio of their areas.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The number of kilometres on the ground represented by lcm or the map
If ΔABC ~ ΔPQR and ∠A = 60°, then ∠P = ?
In figure, PQ is parallel to BC, AP : AB = 2 : 7. If QC = 0 and BC = 21,
Find
(i) AQ
(ii) PQ
Find the scale factor in each of the following and state the type of size transformation:
Actual length = 12cm, Image length = 15cm.
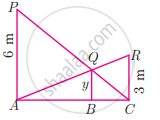
Two vertical poles of heights 6 m and 3 m are erected above a horizontal ground AC. Find the value of y
In ΔABC, AP ⊥ BC and BQ ⊥ AC, B−P−C, A−Q−C, then show that ΔCPA ~ ΔCQB. If AP = 7, BQ = 8, BC = 12, then AC = ?

In ΔCPA and ΔCQB
∠CPA ≅ [∠ ______] ...[each 90°]
∠ACP ≅ [∠ ______] ...[common angle]
ΔCPA ~ ΔCQB ......[______ similarity test]
`"AP"/"BQ" = (["______"])/"BC"` .......[corresponding sides of similar triangles]
`7/8 = (["______"])/12`
AC × [______] = 7 × 12
AC = 10.5
