Advertisements
Advertisements
प्रश्न
In the adjoining figure, the medians BD and CE of a ∆ABC meet at G. Prove that
(i) ∆EGD ∼ ∆CGB and
(ii) BG = 2GD for (i) above.
उत्तर
Since D and E are mid-point of AC and AB respectively in ∆ABC, Ed is parallel to BC.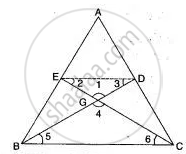
(i) In ∆'s EGD and CGB,
∠EGD = ∠CGB ...(Vertically opp., angles)
∠EGD = ∠CBG ...(Alternative angles)
So, ∆EGD ∼ ∆CGB.
Hence proved.
(ii) ∴ `"BG"/"GD" = "BC"/"DE"`
But `"BC"/"DE" = 2, "So" "BG"/"GD" = 2`
⇒ BG = 2GD.
Hence Proved.
APPEARS IN
संबंधित प्रश्न
The corresponding altitudes of two similar triangles are 6cm and 9cm respectively. Find the ratio of their areas.
In Δ ABC, D and E are points on the sides AB and AC respectively. If AD= 4cm, DB=4.Scm, AE=6.4cm and EC=7.2cm, find if DE is parallel to BC or not.
A model of a ship is made with a scale factor of 1 : 500. Find
The deck area of the model, if the deck area of the ship is 1500000 m2
D and E are points on the sides AB and AC respectively of a Δ ABC such that DE | | BC and divides Δ ABC into two parts, equal in area. Find `"BD"/"AB"`.
In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.
In ΔABC, point D divides AB in the ratio 5:7, Find: BC, If DE = 2.5cm
AM and DN are the altitudes of two similar triangles ABC and DEF. Prove that: AM : DN = AB : DE.
In ∆LMN, ∠L = 60°, ∠M = 50°. If ∆LMN ~ ∆PQR then the value of ∠R is
In ΔDEF and ΔXYZ, `"DE"/"XY" = "FE"/"YZ"` and ∠E ≅ ∠Y. _______ test gives similarity between ΔDEF and ΔXYZ.

∆ABC ~ ∆PQR. If AM and PN are altitudes of ΔABC and ∆PQR respectively and AB2 : PQ2 = 4 : 9, then AM : PN = ______.
