Advertisements
Advertisements
प्रश्न
AM and DN are the altitudes of two similar triangles ABC and DEF. Prove that: AM : DN = AB : DE.
उत्तर
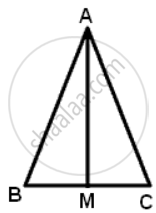
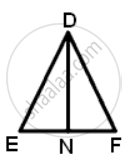
Since ΔABC ∼ ΔDEF
∠B = ∠E
∠AMB = ∠DNE ...(Both are right angles)
Therefore, ΔANB ∼ ΔDNE
∴ `"AM"/"DN" = "AB"/"DE"`
⇒ AM : DN = AB:DE.
APPEARS IN
संबंधित प्रश्न
In figure, if ∠A = ∠C, then prove that ∆AOB ~ ∆COD

In figure, ∠BAC = 90º and segment AD ⊥ BC. Prove that AD2 = BD × DC.
In ∆ABC and ∆DEF ∠B = ∠E, ∠F = ∠C and AB = 3DE then which of the statements regarding the two triangles is true ?
In the figure , ABCD is a quadrilateral . F is a point on AD such that AF = 2.1 cm and FD = 4.9 cm . E and G are points on AC and AB respectively such that EF || CD and GE || BC . Find `("Ar" triangle "BCD")/("Ar" triangle "GEF")`

Δ ABC is similar to Δ PQR. If AB = 6cm, BC = 9cm, PQ = 9cm and PR = 10.5cm, find the lengths of AC and QR.
In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AE)/(AC)`

Prove that the external bisector of an angle of a triangle divides the opposite side externally n the ratio of the sides containing the angle.
In a right-angled triangle ABC, ∠B = 90°, P and Q are the points on the sides AB and AC such as PQBC, AB = 8 cm, AQ = 6 cm and PA:AB = 1:3. Find the lengths of AC and BC.
If ∆ABC – ∆PQR in which ∠A = 53° and ∠Q = 77°, then ∠R is
If ΔABC ~ ΔLMN and ∠A = 60° then ∠L = ?
