Advertisements
Advertisements
प्रश्न
Δ ABC is similar to Δ PQR. If AB = 6cm, BC = 9cm, PQ = 9cm and PR = 10.5cm, find the lengths of AC and QR.
उत्तर
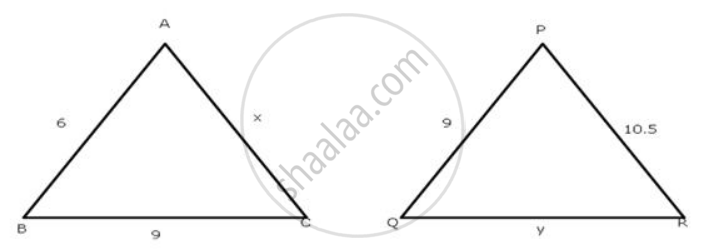
Given : Δ ABC ∼ Δ PQR
To find : AC and QR
Sol : Δ ABC ∼ Δ PQR
`therefore "AB"/"PQ" = "BC"/"QR" = "AC"/"PR"` (Similar sides of similar triangles)
`6/9 = 9/"y" = "x"/10.5`
`6/9 = 9/"y"` `6/9 = "x"/10.5`
⇒ 6y = 81 ⇒ 63 = 9x
⇒ y = `81/6` ⇒ x = 7
⇒ y = `27/2` ⇒ AC = 7 cm
⇒ QR = 13.5 cm
APPEARS IN
संबंधित प्रश्न
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
`triangleDEF ~ triangleMNK`. If DE = 5 and MN = 6, then find the value of `(A(triangleDEF))/(A(triangleMNK))`
E and F are the points in sides DC and AB respectively of parallelogram ABCD. If diagonal AC
and segment EF intersect at G; prove that:
In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N.

Find the lengths of PN and RM.
A model of a ship is made with a scale factor of 1 : 500. Find
The length of the ship, if the model length is 60 cm.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The number of kilometres on the ground represented by lcm or the map
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆RPN

If ∆ABC ~ ∆DEF such that area of ∆ABC is 9 cm2 and the area of ∆DEF is 16 cm2 and BC = 2.1 cm. Find the length of EF.
State whether the following triangles are similar or not: If yes, then write the test of similarity.
∠P = 35°, ∠X = 35° and ∠Q = 60°, ∠Y = 60°

