Advertisements
Advertisements
प्रश्न
The corresponding altitudes of two similar triangles are 6cm and 9cm respectively. Find the ratio of their areas.
उत्तर
Let the two triangles be ABC and DEF with altitudes AP and DQ, respectively.
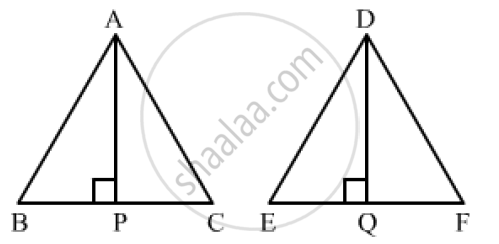
It is given that Δ ABC ~ Δ DEF.
We know that the ration of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
`(ar(ΔABC))/(ar(ΔDEF))=(AP)^2/(DQ)^2`
⇒ `(ar(ΔABC))/(ar(ΔDEF))=6^2/9^2`
=`36/81`
=`4/9`
Hence, the ratio of their areas is 4 : 9
APPEARS IN
संबंधित प्रश्न
In figure, ∠BAC = 90º and segment AD ⊥ BC. Prove that AD2 = BD × DC.
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR:
PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
In the following figure, if LM || CB and LN || CD, prove that `("AM")/("AB")=("AN")/("AD")`

Show that ΔABC, where A(–2, 0), B(2, 0), C(0, 2) and ΔPQR where P(–4, 0), Q(4, 0), R(0, 2) are similar triangles
State, true or false:
All isosceles triangles are similar.
In the given figure, ΔODC~ΔOBA, ∠BOC = 115° and ∠CDO = 700.
Find (i) ∠DCO (ii) ∠DCO (iii) ∠OAB (iv) ∠OBA.

ΔABC~ΔDEF and their areas are respectively 64 cm2 and 121cm2. If EF = 15.4cm, find BC.
In the given figure, DE║BC. If DE = 3cm, BC = 6cm and ar(ΔADE) = `15cm^2`, find the area of ΔABC.

State the SSS-similarity criterion for similarity of triangles
In the given figure, ∠PQR = ∠PST = 90° ,PQ = 5cm and PS = 2cm.
(i) Prove that ΔPQR ~ ΔPST.
(ii) Find Area of ΔPQR : Area of quadrilateral SRQT.

Δ ABC ~ Δ DEF. If BC = 3cm , EF=4cm and area of Δ ABC = 54 cm2 , find area of Δ DEF.
Δ ABC - Δ XYZ. If area of Δ ABC is 9cm2 and area of Δ XYZ is 16cm2 and if BC= 2.1cm, find the length of YZ.
Figure shows Δ KLM , P an T on KL and KM respectively such that∠ KLM =∠ KTP.
If `"KL"/"KT" = 9/5` , find `("Ar" triangle "KLM")/("Ar" triangle "KTP")`.

D and E are points on the sides AB and AC respectively of Δ ABC such that AB=5.6cm, AD= 1.4cm, AC=7 .2cm and AE = 1.5 cm, show that DE is parallel to BC
In Δ ABC, D and E are points on the sides AB and AC respectively. If AD= 4cm, DB=4.Scm, AE=6.4cm and EC=7.2cm, find if DE is parallel to BC or not.
In the following figure, M is mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that : PE = 2 PD

If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AB = 10.8cm, BD = 4.5cm, AC = 4.8cm, and AE = 2.8cm
In the figure, PR || SQ. If PR = 10cm, PT = 5cm, TQ = 6cm and ST = 9cm, calculate RT and SQ.
A map is drawn to scale of 1:20000. Find: The distance on the map representing 4km
A model of a ship is made to a scale of 1:500. Find: The area other deck o the ship, if the area of the deck of its model is m2
Check whether the triangles are similar and find the value of x
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆QMO ~ ∆RPN

In the adjacent figure ∠BAC = 90° and AD ⊥ BC then

In the given figure, if ΔEAT ~ ΔBUN, find the measure of all angles.
If in triangles PQR and XYZ, `"PQ"/"XY" = "QR"/"ZX"` then they will be similar if
In fig. BP ⊥ AC, CQ ⊥ AB, A−P−C, and A−Q−B then show that ΔAPB and ΔAQC are similar.
In ΔAPB and ΔAQC
∠APB = [ ]° ......(i)
∠AQC = [ ]° ......(ii)
∠APB ≅ ∠AQC .....[From (i) and (ii)]
∠PAB ≅ ∠QAC .....[______]
ΔAPB ~ ΔAQC .....[______]
In the given figure the value of x is
In ∠BAC = 90° and AD ⊥ BC. A then ______.

If ΔABC ∼ ΔDEF and ∠A = 48°, then ∠D = ______.
