Question

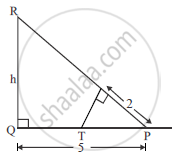
In the given figure,  ∠PQR = ∠PST = 90°  ,PQ = 5cm and PS =  2cm.
(i) Prove that ΔPQR ~ ΔPST.
(ii) Find Area of ΔPQR : Area of quadrilateral SRQT. 

Answer 1

To prove ΔPQR ∼ ΔPST 

In ΔPQR and ΔPST 

∠PQR = ∠PST = 90°

∠P = ∠P               ( common )

∴ ΔPQR ∼ ΔPST               {by AA axiom}

(ii) `("Area of PQR ")/("Area of Quadrilateral")` = 

`("ar" (ΔPQR))/("ar" (ΔPST )) = (1/2 xx PQ xx QR )/(1/2 xxPS xx ST) = 5/2 xx 5/2`

`("ar" (ΔPQR))/("ar" (ΔPST )) = 25/4 [ ∵ (PQ)/(PS) = (QR)/(ST) ]`

Taking the reciprocals on both sides

`("ar" (ΔPST ))/("ar" (ΔPQR)) = 4/25`

Now deducting both sides by 1

` therefore 1 - ("ar" (ΔPST ))/("ar" (ΔPQR)) = 1-4/25`

`("ar" (ΔPQR )- "ar" (ΔPST)) /("ar"(ΔPQR)) = 21/25`

`⇒ ("Area of quadrilateral")/("ar"(Delta PQR)) = 21/25`