Advertisements
Advertisements
प्रश्न
The corresponding sides of two similar triangles ABC and DEF are BC = 9.1cm and EF = 6.5cm. If the perimeter of ΔDEF is 25cm, find the perimeter of ΔABC.
उत्तर
It is given that Δ ABC - Δ DEF.
Therefore, their corresponding sides will be proportional.
Also, the ratio of the perimeters of similar triangles is same as the ratio of their corresponding sides.
⇒ `("Perimeter of ΔABC")/("Perimete of ΔDEF")=(BC)/(EF)`
Let the perimeter of ΔABC be X cm Therefore,
`x/25=9.1/6.5`
`⇒x=(9.1xx25)/6.5=35`
Thus, the perimeter of ΔABC is 35 cm.
APPEARS IN
संबंधित प्रश्न
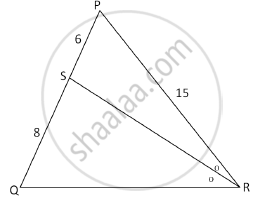
In the following figure, in ΔPQR, seg RS is the bisector of ∠PRQ. If PS = 6, SQ = 8, PR = 15, find QR.
See the given figure. DE || BC. Find AD.

ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :

- ΔADE ∼ ΔACB.
- If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
- Find, area of ΔADE : area of quadrilateral BCED.
In the given figure ABC is a triangle with ∠EDB = ∠ACB. Prove that Δ ABC ~ Δ EBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm. And area of Δ BED = 9 cm2. Calculate the
(1) length of AB
(2) area of Δ ABC

The perimeter of two similar triangles ABC and PQR are 32cm and 24cm respectively. If PQ = 12cm, find AB.
Two chords AB and CD of a circle intersect at a point P outside the circle.
Prove that: (i) Δ PAC ~ Δ PDB (ii) PA. PB = PC.PD

In the given figure, DE║BC and DE: BC = 3:5. Calculate the ratio of the areas of ΔADE and the trapezium BCED.

State the AA-similarity criterion
In Δ ABC , DE is parallel to BC and `"AD"/"DB" = 2/7` IF AC = 5 .6 , find AE.
In Δ ABC, D and E are points on the sides AB and AC respectively. If AD= 4cm, DB=4.Scm, AE=6.4cm and EC=7.2cm, find if DE is parallel to BC or not.
A model of a ship is made with a scale factor of 1 : 500. Find
The volume of the ship, if the volume of its model is 200 cm3.
The actual area of an island is 1872km2 . On a map, this area is 117 cm2. if the length of the coastline is 44cm on the map, find the length of its actual coastline.
A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate : the length of C' A' if CA = 4 cm.
In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find :
- `(CP)/(PA)`
- PQ
- If AP = x, then the value of AC in terms of x.

In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find : If AP = x, then the value of AC in terms of x.

In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y.

Construct a ΔABC in which CA = 6 cm, AB = 5 cm and ∠BAC = 45°. Then construct a triangle whose sides are `3/5` of the corresponding sides of ΔABC.
If ΔPQR, AB is drawn parallel to QR. If PQ = 9cm, PR = 6cm and PB = 4.cm, find the length of AP.
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: The area of ΔAQP.
Find the scale factor in each of the following and state the type of size transformation:
Image length = 8cm, Actual length = 20cm.
Find the scale factor in each of the following and state the type of size transformation:
Model area = 75cm2, Actual area = 3cm2
A plot of land of area 20km2 is represented on the map with a scale factor of 1:200000. Find: The number of KM represented by 2cm on the map.
If in triangles ABC and EDF, `"AB"/"DE" = "BC"/"FD"` then they will be similar, when
In the adjacent figure ∠BAC = 90° and AD ⊥ BC then

ΔPQR ~ ΔSUV. Write pairs of congruent angles
In Quadrilateral ABCD, side AD || BC, diagonal AC and BD intersect in point P, then prove that `"AP"/"PD" = "PC"/"BP"`
In the given figure ΔABC ~ ΔPQR. The value of x is
 |
 |
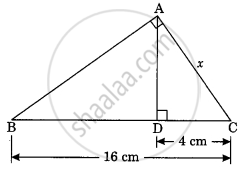
In the given figure the value of x is
The ratio of the corresponding altitudes of two similar triangles is `3/5`. Is it correct to say that ratio of their areas is `6/5`? Why?
Prove that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
Using the above theorem prove that a line through the point of intersection of the diagonals and parallel to the base of the trapezium divides the non-parallel sides in the same ratio.
