Advertisements
Advertisements
प्रश्न
In the given figure ABC is a triangle with ∠EDB = ∠ACB. Prove that Δ ABC ~ Δ EBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm. And area of Δ BED = 9 cm2. Calculate the
(1) length of AB
(2) area of Δ ABC

उत्तर
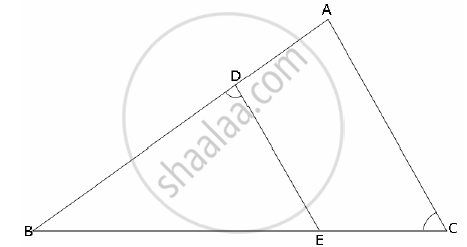
In Δ ABC and Δ EBD,
∠ACB = ∠EDB (given)
∠ABC = ∠EBD (common)
∠ABC ~ ∠EBD (by AA- similarity).
1) We have `(AB)/(BE) = (BC)/(BD) => AB = (6 xx 10)/5 = 12 cm`
2)`"Area of Δ ABC"/"Area of Δ BED" = ((AB)/(BE))^2`
=> Area of Δ ABC =`(12/6)^2 xx 9 cm = 4 xx 9 cm^2 = 36 cm^2`
APPEARS IN
संबंधित प्रश्न
In figure, `\frac{AO}{OC}=\frac{BO}{OD}=\frac{1}{2}` and AB = 5 cm. Find the value of DC.
Given: ∠GHE = ∠DFE = 90°,
DH = 8, DF = 12,
DG = 3x – 1 and DE = 4x + 2.

Find: the lengths of segments DG and DE.
In the given figure, BC is parallel to DE. Area of triangle ABC = 25 cm2, Area of trapezium BCED = 24 cm2 and DE = 14 cm. Calculate the length of BC. Also, find the area of triangle BCD.

In the given figure, ∠ABC = 90° and BD⊥AC. If AB = 5.7cm, BD = 3.8cm and CD = 5.4cm, find BC.
ΔABC is right angled at A and AD⊥BC. If BC = 13cm and AC = 5cm, find the ratio of the areas of ΔABC and ΔADC.
If in ∆DEF and ∆PQR, ∠D ≅ ∠Q, ∠R ≅ ∠E then which of the following statements is false?

A triangle LMN has been reduced by scale factor 0.8 to the triangle L' M' N'. Calculate: the length of M' N', if MN = 8 cm.
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
If ΔPQR, AB is drawn parallel to QR. If PQ = 9cm, PR = 6cm and PB = 4.cm, find the length of AP.
State whether the following triangles are similar or not: If yes, then write the test of similarity.
∠P = 35°, ∠X = 35° and ∠Q = 60°, ∠Y = 60°

