Advertisements
Advertisements
Question
In the given figure ABC is a triangle with ∠EDB = ∠ACB. Prove that Δ ABC ~ Δ EBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm. And area of Δ BED = 9 cm2. Calculate the
(1) length of AB
(2) area of Δ ABC

Solution
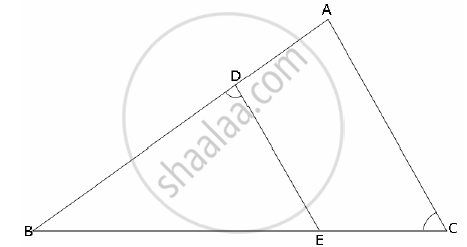
In Δ ABC and Δ EBD,
∠ACB = ∠EDB (given)
∠ABC = ∠EBD (common)
∠ABC ~ ∠EBD (by AA- similarity).
1) We have `(AB)/(BE) = (BC)/(BD) => AB = (6 xx 10)/5 = 12 cm`
2)`"Area of Δ ABC"/"Area of Δ BED" = ((AB)/(BE))^2`
=> Area of Δ ABC =`(12/6)^2 xx 9 cm = 4 xx 9 cm^2 = 36 cm^2`
APPEARS IN
RELATED QUESTIONS
In figure, ABCD is a trapezium with AB || DC. If ∆AED is similar to ∆BEC, prove that AD = BC.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that `("AO")/("BO") = ("CO")/("DO")`. Show that ABCD is a trapezium.
State, true or false:
Two similar polygons are necessarily congruent.
P and Q are points on the sides AB and AC respectively of a ΔABC. If AP = 2cm, PB = 4cm, AQ = 3cm and QC = 6cm, show that BC = 3PQ.
In the given figure, ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1cm, PB = 3cm, AQ = 1.5cm, QC = 4.5cm, prove that area of ΔAPQ is 116 of the area of ΔABC.
If Δ ABC , MN || BC .

If AN : AC= 5 : 8, find ar(Δ AMN) : ar(Δ ABC)
In Δ PQR, MN is drawn parallel to QR. If PM = x, MQ = (x-2), PN = (x+2) and NR = (x-1), find the value of x.
In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AE)/(AC)`

In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4x - 3, AE = 8x - 7, BD = 3x - 1 and CE = 5x - 3,Find x.
In the adjacent figure ∠BAC = 90° and AD ⊥ BC then

