Question

In MBC, DE is drawn parallel to BC. If AD: DB=2:3, DE =6cm and AE =3.6cm, find BC and AC. 

Answer 1

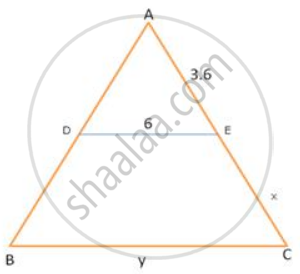
Given : DE = 6 cm , AE = 3.6 cm , `"AD"/"DB" = 2/3` , DE || BC

To find : BC  and AC 

Sol : In Δ ABC , DE || BC

∴ By BPT `"AD"/"DB" = "AE"/"EC"`

`2/3 = 3.6/"x"`

x = `(3.6 xx 2)/2`

= 1.8 × 3

x = 5.4 = EC

∴ AC = 3.6 + 5.4 = 9 cm

AC = 9 cm

In ΔADE and Δ ABC

∠ ADE = ∠ ABC

Similarly ∠AED = ∠ ACB (corresponding angles)

∴ ΔADE ∼ Δ ABC    (AA corollary)

`"AE"/"AC" = "DE"/"BC"` (similar sides of angles)

`3.6/9 = 6 /"y"`

y = `(9 xx 6)/3.6`

y = 15

BC = 15 cm