Advertisements
Advertisements
प्रश्न
Δ ABC - Δ XYZ. If area of Δ ABC is 9cm2 and area of Δ XYZ is 16cm2 and if BC= 2.1cm, find the length of YZ.
उत्तर

Given : Δ ABC ∼ Δ XYZ
To find : YZ
Sol : `("Ar" triangle "ABC")/("Ar" triangle "XYZ") = ("BC"^2)/("YZ"^2)`
[The ration of areas of two similar triangle is equal to the ratio of square of their corresponding sides.]
`9/16 = (2.1)^2/"YZ"^2`
Taking square root both sides ,
`3/4 = 2.1/"YZ"`
YZ = `(2.1 xx 4)/3`
YZ = 2.8 cm
APPEARS IN
संबंधित प्रश्न
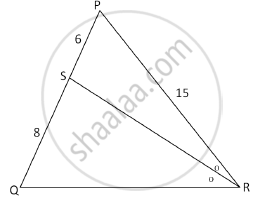
In the following figure, in ΔPQR, seg RS is the bisector of ∠PRQ. If PS = 6, SQ = 8, PR = 15, find QR.
In the given figure, ∠ABC = 75°, ∠EDC = 75° state which two triangles are similar and by which test? Also write the similarity of these two triangles by a proper one to one correspondence.

Figure shows Δ PQR in which ST || QR and SR and QT intersect each other at M. If `"PT"/"TR" = 5/3` find `("Ar" (triangle "MTS"))/("Ar" (triangle "MQR"))`

A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
In the given figure, ABC is a triangle. DE is parallel to BC and `"AD"/"DB" = (3)/(2)`.
(i) Determine the ratios `"AD"/"AB","DE"/"BC"`.
(ii) Prove that ΔDEF is similar to ΔCBF.
Hence, find `"EF"/"FB"`.
(iii) What is the ratio of the areas of ΔDEF and ΔBFC?
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AD"/"AB"`
In ΔABC, point D divides AB in the ratio 5:7, Find: BC, If DE = 2.5cm
If ΔPQR, AB is drawn parallel to QR. If PQ = 9cm, PR = 6cm and PB = 4.cm, find the length of AP.
In the adjacent figure ∠BAC = 90° and AD ⊥ BC then

