Advertisements
Advertisements
प्रश्न
In the given figure, ABC is a triangle. DE is parallel to BC and `"AD"/"DB" = (3)/(2)`.
(i) Determine the ratios `"AD"/"AB","DE"/"BC"`.
(ii) Prove that ΔDEF is similar to ΔCBF.
Hence, find `"EF"/"FB"`.
(iii) What is the ratio of the areas of ΔDEF and ΔBFC?
उत्तर
(i) Given
DE || BC
and `"AD"/"DB" = (3)/(2)`
In ΔADE and ΔABC,
∠A = ∠A, ...(Common Angles)
∠D = ∠B ...(Corresponding Angles)
∴ ΔADE ∼ ΔABC ...(by A.A. criterion)
∴ `"AD"/"AB" = "AE"/"AC" = "DE"/"BC"`
Now `"AD"/"AB" = "AD"/("AD"+"BC")`
= `(3)/(3 + 2) = (3)/(5)`
∴ `"AD"/"AB" = (3)/(5) = "DE"/"BC"`.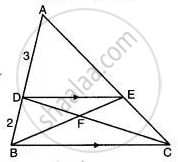
(ii) In ΔDEF and ΔCBF,
∠FDE = ∠FCB ...(Alternate Angle)
∠DFE = ∠BFC ...(Vertically Opposite Angle)
∴ ΔDEF ∼ ΔCBF ...(by A.A. criterion)
Hence proved.
`"EF"/"FB" = "DE"/"BC" = (3)/(5)`
∴ `"EF"/"FB" = (3)/(5)`.
(iii) `"Area of ΔDFE"/"Area of ΔCBF" = "EF"^2/"FB"^2 = 3^2/5^2 = (9)/(25)`.
APPEARS IN
संबंधित प्रश्न
In the given figure, QR is parallel to AB and DR is parallel to AB and DR is parallel to QB.

Prove that: PQ2 = PD × PA.
In the given triangle P, Q and R are the mid-points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5cm, find the length of QR.
In figure , DEF is a right -angled triangle with ∠ E = 90 °.FE is produced to G and GH is drawn perpendicular to DE = 8 cm , DH = 8 cm ,DH = 6 cm and HF = 4 cm , find `("Ar" triangle "DEF")/("Ar" triangle "GHF")`

The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The number of kilometres on the ground represented by lcm or the map
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 11, SQ = 12, PR = 22. Find QR.

On a map drawn to scale of 1 : 2,50,000 a rectangular plot of land ABCD has the following measurement AB = 12 cm, BC = 16 cm angles A, B, C, and D are 900 each. Calculate:
(i) The diagonal distance of the plot of land in
(ii) Actual length of diagonal.
In the figure, PR || SQ. If PR = 10cm, PT = 5cm, TQ = 6cm and ST = 9cm, calculate RT and SQ.
Find the scale factor in each of the following and state the type of size transformation:
Actual area = 64m2, Model area = 100cm2
A plot of land of area 20km2 is represented on the map with a scale factor of 1:200000. Find: The area on the map that represented the plot of land.
