Advertisements
Advertisements
Question
In the given figure, ABC is a triangle. DE is parallel to BC and `"AD"/"DB" = (3)/(2)`.
(i) Determine the ratios `"AD"/"AB","DE"/"BC"`.
(ii) Prove that ΔDEF is similar to ΔCBF.
Hence, find `"EF"/"FB"`.
(iii) What is the ratio of the areas of ΔDEF and ΔBFC?
Solution
(i) Given
DE || BC
and `"AD"/"DB" = (3)/(2)`
In ΔADE and ΔABC,
∠A = ∠A, ...(Common Angles)
∠D = ∠B ...(Corresponding Angles)
∴ ΔADE ∼ ΔABC ...(by A.A. criterion)
∴ `"AD"/"AB" = "AE"/"AC" = "DE"/"BC"`
Now `"AD"/"AB" = "AD"/("AD"+"BC")`
= `(3)/(3 + 2) = (3)/(5)`
∴ `"AD"/"AB" = (3)/(5) = "DE"/"BC"`.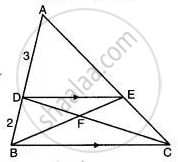
(ii) In ΔDEF and ΔCBF,
∠FDE = ∠FCB ...(Alternate Angle)
∠DFE = ∠BFC ...(Vertically Opposite Angle)
∴ ΔDEF ∼ ΔCBF ...(by A.A. criterion)
Hence proved.
`"EF"/"FB" = "DE"/"BC" = (3)/(5)`
∴ `"EF"/"FB" = (3)/(5)`.
(iii) `"Area of ΔDFE"/"Area of ΔCBF" = "EF"^2/"FB"^2 = 3^2/5^2 = (9)/(25)`.
APPEARS IN
RELATED QUESTIONS
In the given triangle P, Q and R are the mid-points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

The areas of two similar triangles are `64cm^2` and `100cm^2` respectively. If a median of the smaller triangle is 5.6cm, find the corresponding median of the other.
Are the triangles in the given figure similar? If yes, by which test?

In the given figure, A – D – C and B – E – C seg DE || side AB If AD = 5, DC = 3, BC = 6.4 then Find BE.

A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in cm, of the model; if the length of the aeroplane is 40 m.
Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The area of land represented on the map.
If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is

In ΔABC, DE || BC (as shown in the figure), If AD = 4 cm, AB = 9 cm and AC = 13.5 cm, then the length of EC is ______.
