Advertisements
Advertisements
प्रश्न
In the given figure, ABC is a triangle. DE is parallel to BC and `"AD"/"DB" = (3)/(2)`.
(i) Determine the ratios `"AD"/"AB","DE"/"BC"`.
(ii) Prove that ΔDEF is similar to ΔCBF.
Hence, find `"EF"/"FB"`.
(iii) What is the ratio of the areas of ΔDEF and ΔBFC?
उत्तर
(i) Given
DE || BC
and `"AD"/"DB" = (3)/(2)`
In ΔADE and ΔABC,
∠A = ∠A, ...(Common Angles)
∠D = ∠B ...(Corresponding Angles)
∴ ΔADE ∼ ΔABC ...(by A.A. criterion)
∴ `"AD"/"AB" = "AE"/"AC" = "DE"/"BC"`
Now `"AD"/"AB" = "AD"/("AD"+"BC")`
= `(3)/(3 + 2) = (3)/(5)`
∴ `"AD"/"AB" = (3)/(5) = "DE"/"BC"`.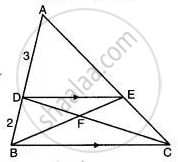
(ii) In ΔDEF and ΔCBF,
∠FDE = ∠FCB ...(Alternate Angle)
∠DFE = ∠BFC ...(Vertically Opposite Angle)
∴ ΔDEF ∼ ΔCBF ...(by A.A. criterion)
Hence proved.
`"EF"/"FB" = "DE"/"BC" = (3)/(5)`
∴ `"EF"/"FB" = (3)/(5)`.
(iii) `"Area of ΔDFE"/"Area of ΔCBF" = "EF"^2/"FB"^2 = 3^2/5^2 = (9)/(25)`.
APPEARS IN
संबंधित प्रश्न
Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
A line PQ is drawn parallel to the base BC of ∆ABC which meets sides AB and AC at points P and Q respectively. If AP = `1/3` PB; find the value of:
- `"Area of ΔABC"/"Area of ΔAPQ"`
- `"Area of ΔAPQ"/"Area of trapezium PBCQ"`
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The number of kilometres on the ground represented by lcm or the map
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : A' B', if AB = 4 cm.
ΔXYZ is enlarged to ΔX'Y'Z'. If XY = 12cm, YZ = 8cm and XZ = 14cm and the smallest side of ΔX'Y'Z' is 12cm, find the scale factor and use it to find the length of the other sides of the image ΔX'Y'Z'.
A model of a ship is made to a scale of 1:500. Find: The area other deck o the ship, if the area of the deck of its model is m2
A girl looks the reflection of the top of the lamp post on the mirror which is 6.6 m away from the foot of the lamppost. The girl whose height is 1.25 m is standing 2.5 m away from the mirror. Assuming the mirror is placed on the ground facing the sky and the girl, mirror and the lamppost are in the same line, find the height of the lamp post.
A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
There are two poles having heights 8 m and 4 m on plane ground as shown in fig. Because of sunlight shadows of smaller pole is 6m long, then find the length of shadow of longer pole.
In the given figure, if ABCD is a trapezium in which AB || CD || EF, then prove that `(AE)/(ED) = (BF)/(FC)`.

