Question

A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?

Answer 1

Let the height of the tree AD be “h”.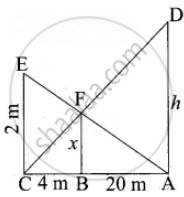

In ∆ACD and ∆BCF,

∠A = ∠B = 90°

∠C is common

∆ACD ~ ∆BCF by AA similarity

`"AD"/"BF" = "AC"/"BC"`

`"h"/x = 24/2` = 6

h = 6x  ...(1)

In ∆ACE and ∆ABF,

∠C = ∠B = 90°

∠A is common

∴ ∆ACE ~ ∆ABF

`"CE"/"BF" = "AC"/"AB"`

`2/x = 24/20`

24x = 20 × 2

x = `(20 xx 2)/24 = (5 xx 2)/6 = 10/6`

x = `5/3`

Substitute the value of x in (1)

h = `6 xx 5/3` = 10 m

∴ Height of the tree is 10 m