Advertisements
Advertisements
प्रश्न
D and E are points on the sides AB and AC respectively of a Δ ABC such that DE | | BC and divides Δ ABC into two parts, equal in area. Find `"BD"/"AB"`.
उत्तर
We have
area (Δ ADE) = area (trapezium BCED)
⇒ area (Δ ADE) + area (Δ ADE)
= area (trapezium BCED) + area (Δ ADE)
⇒ 2 area (Δ ADE) = area (Δ ABC) ...(i)
In Δ ADE and Δ ABC, we have
∠ADE = ∠B, ...[∵ DE | | BC]
∴ ∠AED = ∠C ...(corresponding angles)]
and ∠A = ∠A, ...[Common]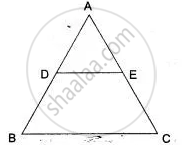
∴ Δ ADE ∼ Δ ABC
⇒ `"area (Δ ADE)"/"area (Δ ABC)" = "AD"^2/"AB"^2`
⇒ `"area (Δ ADE)"/(2"area (Δ ADE)") = "AD"^2/"AB"^2`
⇒ `(1)/(2) = ("AD"/"AB")^2`
⇒ `"AD"/"AB" = (1)/sqrt(2)`
⇒ AB = `sqrt(2)"AD"`
⇒ AB = `sqrt(2)("AB - BD")`
⇒ `(sqrt(2) - 1)"AB" = sqrt(2)"BD"`
⇒ `"BD"/"AB" = (sqrt(2) - 1)/(sqrt(2)`
= `(2 - sqrt(2)/(2))`.
APPEARS IN
संबंधित प्रश्न
In figure, `\frac{AO}{OC}=\frac{BO}{OD}=\frac{1}{2}` and AB = 5 cm. Find the value of DC.
P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm, PB = 6cm. AQ = 5 cm and QC = 10 cm, show that BC = 3PQ.
`triangleDEF ~ triangleMNK`. If DE = 5 and MN = 6, then find the value of `(A(triangleDEF))/(A(triangleMNK))`
ABCD is parallelogram and E is a point on BC. If the diagonal BD intersects AE at F, prove that AF × FB = EF × FD.

Two chords AB and CD of a circle intersect at a point P outside the circle.
Prove that: (i) Δ PAC ~ Δ PDB (ii) PA. PB = PC.PD

In the given figure, seg XY || seg BC, then which of the following statements is true?

In ΔPQR, PQ = 10 cm, QR = 12cm, PR = 8 cm, find the biggest and the smallest angle of the triangle.
In the following figure, M is mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that : PE = 2 PD

The diagonal AC of a parallelogram ABCD intersects DP at the point Q, where P is any point on side AB. Prove that CQ x PQ = QA x QD.
In the given figure ΔABC ~ ΔPQR. The value of x is
 |
 |
