Advertisements
Advertisements
Question
In the given figure, AB and DE are perpendicular to BC.

- Prove that ΔABC ∼ ΔDEC
- If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
- Find the ratio of the area of a ΔABC : area of ΔDEC.
Solution
i. Given AB ⊥ BC
DE ⊥ BC
To prove: ΔABC ∼ ΔDEC
Proof: If ΔABC and ΔDEC
∠ABC = ∠DEC = 90°each ...(Given)
∠C = ∠C ...(Common)
∴ ΔABC ∼ ΔDEC ...(AA criterion)
Hence proved.
ii. AB = 6 cm, DE = 4 cm
AC = 15 cm, CD = ?
Since ΔABC ∼ ΔDEC
`=> (AB)/(DE) = (AC)/(CD)` ...(Corresponding sides of similar Δ's are proportional)
∴ `(6)/(4) = (15)/(CD)`
`=> CD = (15 xx 4)/(6) = 10`.
iii. `"Area of ΔABC"/"Area of ΔDEC" = (AB^2)/(DE^2)` ...(Area theorem)
= `(36)/(16)`
= `(9)/(4)` or 9 : 4.
APPEARS IN
RELATED QUESTIONS
Examine each pair of triangles in Figure, and state which pair of triangles are similar. Also, state the similarity criterion used by you for answering the question and write the similarity relation in symbolic form
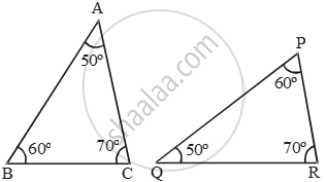
figure (i)
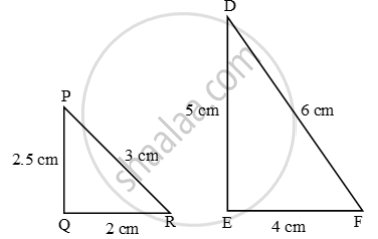
figure 2
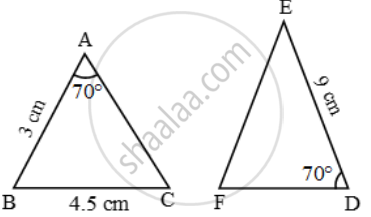
figure 3

figure 4
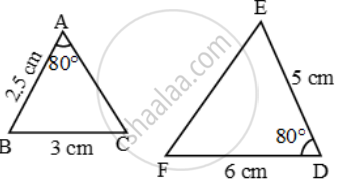
figure 5
figure 6

figure 7
Given: ∠GHE = ∠DFE = 90°,
DH = 8, DF = 12,
DG = 3x – 1 and DE = 4x + 2.

Find: the lengths of segments DG and DE.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5,

Find:
- ∆APB : ∆CPB
- ∆DPC : ∆APB
- ∆ADP : ∆APB
- ∆APB : ∆ADB
The two similar triangles are equal in area. Prove that the triangles are congruent.
In the given figure, ∠1 = ∠2 and `(AC)/(BD)=(CB)/(CE)` Prove that Δ ACB ~ Δ DCE.
In the given figure, seg XY || seg BC, then which of the following statements is true?

In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AD)/(AB)`

The model of a building is constructed with scale factor 1:30.
(i) If the height of the model is 80 cm, find the actual height of the building in metres.
(ii) If the actual volume of a tank at the top of the building is 27 m3, find the volume of the tank on the top of the model.
On a map drawn to scale of 1 : 2,50,000 a rectangular plot of land ABCD has the following measurement AB = 12 cm, BC = 16 cm angles A, B, C, and D are 900 each. Calculate:
(i) The diagonal distance of the plot of land in
(ii) Actual length of diagonal.
The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is
