Advertisements
Advertisements
Question
In MBC, DE is drawn parallel to BC. If AD: DB=2:3, DE =6cm and AE =3.6cm, find BC and AC.
Solution
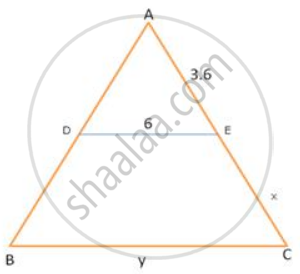
Given : DE = 6 cm , AE = 3.6 cm , `"AD"/"DB" = 2/3` , DE || BC
To find : BC and AC
Sol : In Δ ABC , DE || BC
∴ By BPT `"AD"/"DB" = "AE"/"EC"`
`2/3 = 3.6/"x"`
x = `(3.6 xx 2)/2`
= 1.8 × 3
x = 5.4 = EC
∴ AC = 3.6 + 5.4 = 9 cm
AC = 9 cm
In ΔADE and Δ ABC
∠ ADE = ∠ ABC
Similarly ∠AED = ∠ ACB (corresponding angles)
∴ ΔADE ∼ Δ ABC (AA corollary)
`"AE"/"AC" = "DE"/"BC"` (similar sides of angles)
`3.6/9 = 6 /"y"`
y = `(9 xx 6)/3.6`
y = 15
BC = 15 cm
APPEARS IN
RELATED QUESTIONS
In figure, QA and PB are perpendicular to AB. If AO = 10 cm, BO = 6 cm and PB = 9 cm. Find AQ
In the given figure, ∠ABC = 90° and BD⊥AC. If AB = 5.7cm, BD = 3.8cm and CD = 5.4cm, find BC.
In the given figure, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF.

Proof : In ΔXDE, PQ || DE ...`square`
∴ `"XP"/square = square/"QE"` ...(I) (Basic proportionality theorem)
In ΔXEF, QR || EF ...`square`
∴ `square/square = square/square ..."(II)" square`
∴ `square/square = square/square` ...from (I) and (II)
∴ seg PR || seg DF ...(converse of basic proportionality theorem)
Construct a triangle ABC with side BC = 6 cm, ∠B = 45°, ∠A = 105°. Then construct another triangle whose sides are `(3)/(4)` times the corresponding sides of the ΔABC.
The sides PQ and PR of the ΔPQR are produced to S and T respectively. ST is drawn parallel to QR and PQ: PS = 3:4. If PT = 9.6 cm, find PR. If 'p' be the length of the perpendicular from P to QR, find the length of the perpendicular from P to ST in terms of 'p'.
Two figures are similar. If the ratio of their perimeters is 8:16. What will be the ratio of the corresponding sides?
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The diagonal distance of the plot in km
If figure OPRQ is a square and ∠MLN = 90°. Prove that QR2 = MQ × RN

ΔABP ~ ΔDEF and A(ΔABP) : A(ΔDEF) = 144:81, then AB : DE = ?
In the given figure, ∠ACB = ∠CDA, AC = 8cm, AD = 3cm, then BD is ______.

