Advertisements
Advertisements
प्रश्न
In MBC, DE is drawn parallel to BC. If AD: DB=2:3, DE =6cm and AE =3.6cm, find BC and AC.
उत्तर
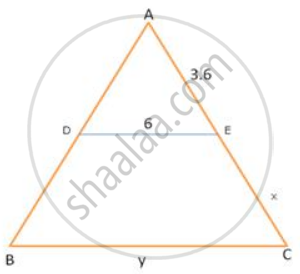
Given : DE = 6 cm , AE = 3.6 cm , `"AD"/"DB" = 2/3` , DE || BC
To find : BC and AC
Sol : In Δ ABC , DE || BC
∴ By BPT `"AD"/"DB" = "AE"/"EC"`
`2/3 = 3.6/"x"`
x = `(3.6 xx 2)/2`
= 1.8 × 3
x = 5.4 = EC
∴ AC = 3.6 + 5.4 = 9 cm
AC = 9 cm
In ΔADE and Δ ABC
∠ ADE = ∠ ABC
Similarly ∠AED = ∠ ACB (corresponding angles)
∴ ΔADE ∼ Δ ABC (AA corollary)
`"AE"/"AC" = "DE"/"BC"` (similar sides of angles)
`3.6/9 = 6 /"y"`
y = `(9 xx 6)/3.6`
y = 15
BC = 15 cm
APPEARS IN
संबंधित प्रश्न
The areas of two similar triangles are `81cm^2` and `49cm^2` respectively. If the altitude of the first triangle is 6.3cm, find the corresponding altitude of the other.
ΔABC ∼ ΔDEF and A(ΔABC) : A Δ(DEF) = 1 : 2 If AB = 4 find DE.
In Δ ABC , MN || BC .

If BC = 14 cm and MN = 6 cm , find `("Ar" triangle "AMN")/("Ar" . ("trapezium MBCN"))`
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find
The area on the map that represents the plot of land.
In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AE)/(AC)`

In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4x - 3, AE = 8x - 7, BD = 3x - 1 and CE = 5x - 3,Find x.
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AD"/"AB"`
AM and DN are the altitudes of two similar triangles ABC and DEF. Prove that: AM : DN = AB : DE.
In the given figure, if ΔEAT ~ ΔBUN, find the measure of all angles.

In ΔABC, DE || BC (as shown in the figure), If AD = 4 cm, AB = 9 cm and AC = 13.5 cm, then the length of EC is ______.
