Advertisements
Advertisements
प्रश्न

In ΔABC, DE || BC (as shown in the figure), If AD = 4 cm, AB = 9 cm and AC = 13.5 cm, then the length of EC is ______.
पर्याय
6 cm
7.5 cm
9 cm
5.7 cm
उत्तर
In ΔABC, DE || BC (as shown in the figure), If AD = 4 cm, AB = 9 cm and AC = 13.5 cm, then the length of EC is 7.5 cm.
Explanation:

Given: AD = 4 cm, AB = 9 cm, and AC = 13.5 cm
Using the properties of similar triangles, when DE || BC, triangles ADE and ABC are similar.
From the similarity of the triangles:
`(AD)/(AB) = (AE)/(AC)`
Now we can express AE in terms of AC, since AE + EC = AC:
`4/9 = (AE)/13.5`
AE = `4/9 xx 13.5`
AE = 6
Now EC will be:
EC = AC − AE
EC = 13.5 − 6
EC = 7.5
APPEARS IN
संबंधित प्रश्न
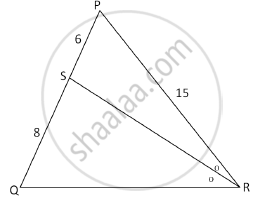
In the following figure, in ΔPQR, seg RS is the bisector of ∠PRQ. If PS = 6, SQ = 8, PR = 15, find QR.
In figure, QA and PB are perpendicular to AB. If AO = 10 cm, BO = 6 cm and PB = 9 cm. Find AQ
In figure, if ∠A = ∠C, then prove that ∆AOB ~ ∆COD

In the following figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
- Prove that ΔACD is similar to ΔBCA.
- Find BC and CD.
- Find area of ΔACD : area of ΔABC.

A line PQ is drawn parallel to the base BC of ∆ABC which meets sides AB and AC at points P and Q respectively. If AP = `1/3` PB; find the value of:
- `"Area of ΔABC"/"Area of ΔAPQ"`
- `"Area of ΔAPQ"/"Area of trapezium PBCQ"`
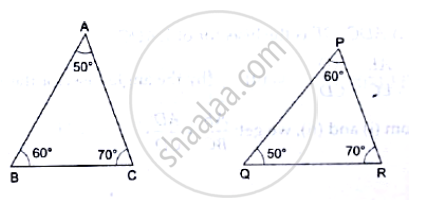
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
The corresponding sides of two similar triangles ABC and DEF are BC = 9.1cm and EF = 6.5cm. If the perimeter of ΔDEF is 25cm, find the perimeter of ΔABC.
ABCD is parallelogram and E is a point on BC. If the diagonal BD intersects AE at F, prove that AF × FB = EF × FD.

In the given figure, DE║BC. If DE = 3cm, BC = 6cm and ar(ΔADE) = `15cm^2`, find the area of ΔABC.

In the following figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and \[\text{AD} = 9 \text{ find} \frac{A\left( \Delta ABE \right)}{A\left( \Delta BAD \right)} \cdot\]

∆ABC and ∆DEF are equilateral triangles, A(∆ABC): A(∆DEF) = 1: 2. If AB = 4 then what is length of DE?

A ship is 400m laig and 100m wide. The length of its model is 20 cm. find the surface area of the deck of the model.
A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate : the length of C' A' if CA = 4 cm.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : A' B', if AB = 4 cm.
Construct a triangle ABC with side BC = 6 cm, ∠B = 45°, ∠A = 105°. Then construct another triangle whose sides are `(3)/(4)` times the corresponding sides of the ΔABC.
In the adjoining figure, the medians BD and CE of a ∆ABC meet at G. Prove that
(i) ∆EGD ∼ ∆CGB and
(ii) BG = 2GD for (i) above.
In ΔABC, DE is drawn parallel to BC cutting AB in the ratio 2 : 3. Calculate:
(i) `("area"(Δ"ADE"))/("area"(Δ"ABC")`
(i) `("area"("trapeziumEDBC"))/("area"(Δ"ABC"))`
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The diagonal distance of the plot in km
Check whether the triangles are similar and find the value of x
In the adjacent figure, ∆ABC is right angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE and hence find the lengths of AE and DE
In the adjacent figure, ∆ACB ~ ∆APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm and AP = 2.8 cm, find CA and AQ

Construct a triangle similar to a given triangle PQR with its sides equal to `7/3` of the corresponding sides of the triangle PQR (scale factor `7/3 > 1`)
State whether the following triangles are similar or not: If yes, then write the test of similarity.
∠P = 35°, ∠X = 35° and ∠Q = 60°, ∠Y = 60°

ΔABC ~ ΔPQR, A(ΔABC) = 80 sq.cm, A(ΔPQR) = 125 sq.cm, then complete `("A"(Δ"ABC"))/("A"(Δ"PQR")) = 80/125 = (["______"])/(["______"])`, hence `"AB"/"PQ" = (["______"])/(["______"])`
There are two poles having heights 8 m and 4 m on plane ground as shown in fig. Because of sunlight shadows of smaller pole is 6m long, then find the length of shadow of longer pole.
In triangle ABC point D is on side BC (B−D−C) such that ∠BAC = ∠ADC then prove that CA2 = CB × CD
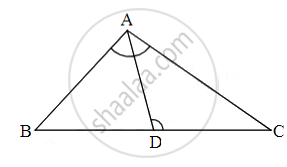
If ∆ABC ~ ∆QRP, `(ar(ABC))/(ar(PQR)) = 9/4`, AB = 18 cm and BC = 15 cm, then PR is equal to ______.
In ΔABC, PQ || BC. If PB = 6 cm, AP = 4 cm, AQ = 8 cm, find the length of AC.

