Advertisements
Advertisements
प्रश्न
In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
- Prove that ΔACD is similar to ΔBCA.
- Find BC and CD.
- Find area of ΔACD : area of ΔABC.

उत्तर
∠ABC = ∠DAC = x ...(Say)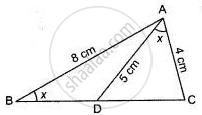
AB = 8 cm,
AC = 4 cm,
AD = 5 cm.
i. In ΔACD and ΔBCA
∠ABC = ∠DAC ...(Given)
∠ACD = ∠BCA ...(Common angles)
`=>` ΔACD ∼ ΔBCA ...(AA criterion for similarity) (i)
Hence ΔACD is similar to ΔBCA.
ii. In ΔACD and ΔBCA
ΔACD ∼ ΔBCA ...[From (i)]
`(AC)/(BC) = (CD)/(CA) = (AD)/(BA)`
`=> (4)/(BC) = (CD)/(4) = (5)/(8)`
`=> (4)/(BC) = (5)/(8)`
`=> BC = (8 xx 4)/(5) = (32)/(5)`
= 6.4 cm
And `(CD)/(4) = (5)/(8)`
`=> CD = (5 xx 4)/(8)`
`=>` CD = 2.5 cm
iii. In ΔACD and ΔBCA
ΔACD ∼ ΔBCA ...[From (i)]
`"Area of ΔACD"/"Area of ΔABC" = ("AC"/"AB")^2`
`=> "Area of ΔACD"/"Area of ΔABC" = 4^2/8^2 = 16/64 = 1/4`
संबंधित प्रश्न
Prove that the line segments joining the mid points of the sides of a triangle form four triangles, each of which is similar to the original triangle
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
State, true or false:
Two isosceles-right triangles are similar.
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

The areas of two similar triangles are `81cm^2` and `49cm^2` respectively. If the altitude of the first triangle is 6.3cm, find the corresponding altitude of the other.
The dimensions of a buiIding are 50 m Iong, 40m wide and 70m high. A model of the same building is made with a scale factor of 1: 500. Find the dimensions of the model.
Points A(3, 1), B(5, 1), C(a, b) and D(4, 3) are vertices of a parallelogram ABCD. Find the values of a and b.
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The diagonal distance of the plot in km
Two triangles QPR and QSR, right angled at P and S respectively are drawn on the same base QR and on the same side of QR. If PR and SQ intersect at T, prove that PT × TR = ST × TQ
If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is
