Advertisements
Advertisements
प्रश्न
Two triangles QPR and QSR, right angled at P and S respectively are drawn on the same base QR and on the same side of QR. If PR and SQ intersect at T, prove that PT × TR = ST × TQ
उत्तर
In ∆PQT and ∆STR we have
∠P = ∠S = 90° ...(Given)
∠PTQ = ∠STR ...(Vertically opposite angle)
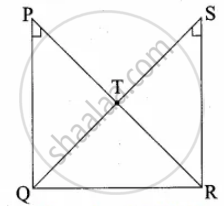
By AA similarity
∆PTQ ~ ∆STR we get
`"PT"/"ST" = "TQ"/"TR"`
PT × TR = ST × TQ
Hence it is proved.
APPEARS IN
संबंधित प्रश्न
Given `triangle ABC ~ triangle PQR`, if `(AB)/(PQ) = 1/3`, then find `(ar triangle ABC)/(ar triangle PQR)`
The actual area of an island is 1872km2 . On a map, this area is 117 cm2. if the length of the coastline is 44cm on the map, find the length of its actual coastline.
The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.

In ΔABC, point D divides AB in the ratio 5:7, Find: BC, If DE = 2.5cm
The dimensions of the model of a building are 1.2m x 75cm x 2m. If the scale factor is 1 : 20; find the actual dimensions of the building.
A map is drawn to scale of 1:20000. Find: The area of the lake on the map which has an actual area of 12km2
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The base area of the truck, if the base area of the model is 30m2
If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is
In the given figure AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y cm. Find x and y.
In ΔPQR, S and T are points on PQ and PR respectively. `(PS)/(SQ) = (PT)/(TR)` and ∠PST = ∠PRQ. Prove that PQR is an isosceles triangle.
