Advertisements
Advertisements
Question
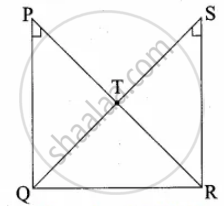
Two triangles QPR and QSR, right angled at P and S respectively are drawn on the same base QR and on the same side of QR. If PR and SQ intersect at T, prove that PT × TR = ST × TQ
Solution
In ∆PQT and ∆STR we have
∠P = ∠S = 90° ...(Given)
∠PTQ = ∠STR ...(Vertically opposite angle)
By AA similarity
∆PTQ ~ ∆STR we get
`"PT"/"ST" = "TQ"/"TR"`
PT × TR = ST × TQ
Hence it is proved.
APPEARS IN
RELATED QUESTIONS
P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm, PB = 6cm. AQ = 5 cm and QC = 10 cm, show that BC = 3PQ.
In the given figure, ∠ABC = 90° and BD⊥AC. If BD = 8cm, AD = 4cm, find CD.
If in ∆DEF and ∆PQR, ∠D ≅ ∠Q, ∠R ≅ ∠E then which of the following statements is false?

In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AE)/(AC)`

Find the area of the triangle ABC with the coordinates of A as (1, −4) and the coordinates of the mid-points of sides AB and AC respectively are (2, −1) and (0, −1).
Given is a triangle with sides 3 cm, 5 cm and 6 cm. Find the sides of a triangle which is similar to the given triangle and its shortest side is 4.5 cm.
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that c2 = `"p"^2 - "a"x + "a"^2/4`
In fig., seg AC and seg BD intersect each other at point P.

`"AP"/"PC" = "BP"/"PD"` then prove that ΔABP ~ ΔCDP
Two triangles are similar. Smaller triangle’s sides are 4 cm, 5 cm, 6 cm. Perimeter of larger triangle is 90 cm then find the sides of larger triangle.
In the given figure, ∠ACB = ∠CDA, AC = 8cm, AD = 3cm, then BD is ______.

