Advertisements
Advertisements
Question
A vertical stick of length 6 m casts a shadow 400 cm long on the ground and at the same time a tower casts a shadow 28 m long. Using similarity, find the height of the tower
Solution
In ∆ABC and ∆PQR,
∠ABC = ∠PQR = 90° ...(Vertical Stick)
∠ACB = ∠PRQ ...(Same time casts shadow)
∆BCA ~ ∆QRP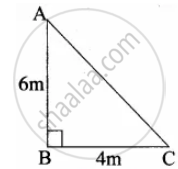
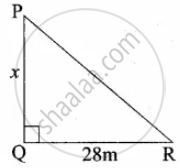
`"AB"/"PQ" = "NC"/"QR"`
`6/x = 4/28`
4x = 6 × 28
⇒ x = `(6 xx 28)/4` = 42
Length of the lamp post = 42 m
APPEARS IN
RELATED QUESTIONS
Prove that the angle bisector of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
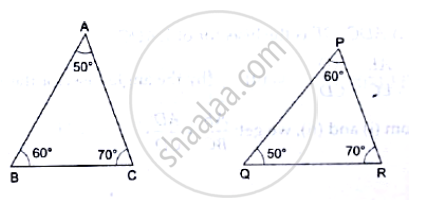
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

As shown in figure, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m then how long will be the shadow of the bigger pole at the same time?

In Δ PQR, MN is drawn parallel to QR. If PM = x, MQ = (x-2), PN = (x+2) and NR = (x-1), find the value of x.
A ship is 400m laig and 100m wide. The length of its model is 20 cm. find the surface area of the deck of the model.
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
In the adjacent figure, ∆ABC is right angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE and hence find the lengths of AE and DE
Construct a triangle similar to a given triangle LMN with its sides equal to `4/5` of the corresponding sides of the triangle LMN (scale factor `4/5 < 1`)
In Quadrilateral ABCD, side AD || BC, diagonal AC and BD intersect in point P, then prove that `"AP"/"PD" = "PC"/"BP"`
