Advertisements
Advertisements
Questions
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then prove that the other two sides are divided in the same ratio.
Solution
Given: Let a ΔABC in which a line DE parallel to BC intersects AB at D and AC at E.
To Prove: DE divides the two sides in the same ratio.
`"AD"/"DB" = "AE"/"EC"`
Construction: Join BE, CD and draw EF ⊥ AB and DG ⊥ AC.
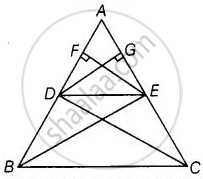
Proof: Here,
Area of triangle = `1/2` × base × height
Area of ΔADE = `1/2` × AD × EF
or
Area of ΔADE = `1/2` × AE × DG
Similarly,
Area of ΔBDE = `1/2` × DB × EF
Area of ΔDEC = `1/2` × EC × DG
`"ar(ΔADE)"/"ar(ΔBDE)" = (1/2 × "AD" × "EF")/(1/2 × "DB" × "EF")`
`"ar(ΔADE)"/"ar(ΔBDE)" = "AD"/"DB"` ...(1)
From (2) and (4),
`"ar(ΔADE)"/"ar(ΔDEC)" = (1/2 × "AE" × "DG")/(1/2 × "EC" × "DG")`
`"ar(ΔADE)"/"ar(ΔDEC)" = "AE"/"EC"` ...(2)
Since, ΔBDE and ΔDEC lie between the same parallel DE and BC and on the same base DE.
∴ ar(ΔBDE) = ar(ΔDEC) ...(3)
From (1), (2) and (3), we get,
`"AD"/"BD" ="AE"/"EC"`
Hence proved.
APPEARS IN
RELATED QUESTIONS
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC in L and AD produced in E. Prove that EL = 2 BL
In figure, ABCD is a trapezium with AB || DC. If ∆AED is similar to ∆BEC, prove that AD = BC.
See the given figure. DE || BC. Find AD.

State, true or false:
Two congruent polygons are necessarily similar.
State, true or false:
Two isosceles-right triangles are similar.
In the given figure, ∆ABC and ∆AMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
- Prove that: ∆ABC ~ ∆AMP
- Find: AB and BC.

∆ABC and ∆DEF are equilateral triangles, A(∆ABC): A(∆DEF) = 1: 2. If AB = 4 then what is length of DE?


O is any point in the interior of ΔABC. Bisectors of ∠AOB, ∠BOC and ∠AOC intersect side AB, side BC, side AC in
F, D and E respectively.
Prove that
BF × AE × CD = AF × CE × BD
Δ ABC - Δ XYZ. If area of Δ ABC is 9cm2 and area of Δ XYZ is 16cm2 and if BC= 2.1cm, find the length of YZ.
In Δ PQR, MN is drawn parallel to QR. If PM = x, MQ = (x-2), PN = (x+2) and NR = (x-1), find the value of x.
An aeroplane is 30m long and its model is l5 cm long. If the total outer surface area of the model is 150 cm2 , find the cost of painting the outer surface of the aeroplane at Rs. 120 per m2, if 5O m2 is left out for windows.
In ΔPQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP.
Prove that : (i) ΔPQL ∼ ΔRPM
(ii) QL. Rm = PL. PM
(iii) PQ2 = QR. QL.
D and E are points on the sides AB and AC respectively of a Δ ABC such that DE | | BC and divides Δ ABC into two parts, equal in area. Find `"BD"/"AB"`.
In the given figure, AB and DE are perpendicular to BC.

- Prove that ΔABC ∼ ΔDEC
- If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
- Find the ratio of the area of a ΔABC : area of ΔDEC.
If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AD = 5.7cm, BD = 9.5cm, AE = 3.3cm, and EC = 5.5cm
In ΔABC, point D divides AB in the ratio 5:7, Find: BC, If DE = 2.5cm
Prove that the external bisector of an angle of a triangle divides the opposite side externally n the ratio of the sides containing the angle.
Through the vertex S of a parallelogram PQRS, a line is drawn to intersect the sides Qp and QR produced at M and N respectively. Prove that `"SP"/"PM" = "MQ"/"QN" = "MR"/"SR"`
D and E are points on the sides AB and AC of ΔABC such that DE | | BC and divides ΔABC into two parts, equal in area. Find `"BD"/"AB"`.
ΔABC is enlarged, with a scale factor 5. Find: A'B', if AB = 4cm
On a map drawn to a scale of 1: 2,50,000, a triangular plot of land has the following measurements:
AB = 3 cm, BC = 4 cm, ∠ABC = 90°. Calculate:
(i) The actual length of AB in km.
(ii) The area of Plot in sq. km.
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The length of the truck
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The base area of the truck, if the base area of the model is 30m2
The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is
In any triangle _______ sides are opposite to equal angles
In fig. BP ⊥ AC, CQ ⊥ AB, A−P−C, and A−Q−B then show that ΔAPB and ΔAQC are similar.
In ΔAPB and ΔAQC
∠APB = [ ]° ......(i)
∠AQC = [ ]° ......(ii)
∠APB ≅ ∠AQC .....[From (i) and (ii)]
∠PAB ≅ ∠QAC .....[______]
ΔAPB ~ ΔAQC .....[______]
It is given that ΔABC ~ ΔPQR, with `(BC)/(QR) = 1/3`. Then, `(ar(PRQ))/(ar(BCA))` is equal to ______.
In the given figure, if ABCD is a trapezium in which AB || CD || EF, then prove that `(AE)/(ED) = (BF)/(FC)`.


In ΔABC, DE || BC (as shown in the figure), If AD = 4 cm, AB = 9 cm and AC = 13.5 cm, then the length of EC is ______.
