Advertisements
Advertisements
Question
In figure, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.
Solution
According to the question,
PQRS is a parallelogram,
Therefore, PQ || SR and PS || QR.
Also given, AB || PS.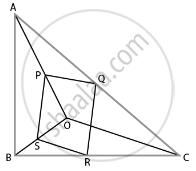
To prove:
OC || SR
From ∆OPS and OAB,
PS || AB
∠POS = ∠AOB ...[Common angle]
∠OSP = ∠OBA ...[Corresponding angles]
∴ ∆OPS ∼ ∆OAB ...[By AAA similarity criteria]
Then,
Using basic proportionality theorem,
We get,
`("PS")/("AB") = ("OS")/("OB")` ...(i)
From ∆CQR and ∆CAB,
QR || PS || AB
∠QCR = ∠ACB ...[Common angle]
∠CRQ = ∠CBA ...[Corresponding angles]
∴ ∆CQR ∼ ∆CAB
Then, by basic proportionality theorem
`("QR")/("AB") = ("CR")/("CB")`
⇒ `("PS")/("AB") = ("CR")/("CB")` ...(ii) [PS ≅ QR Since, PQRS is a parallelogram]
From equations (i) and (ii),
`("OS")/("OB") = ("CR")/("CB")`
or
`("OB")/("OS") = ("CB")/("CR")`
Subtracting 1 from L.H.S and R.H.S, we get,
`("OB")/("OS") - 1 = ("CB")/("CR") - 1`
⇒ `("OB" - "OS")/("OS") = ("CB" - "CR")/("CR")`
⇒ `("BS")/("OS") = ("BR")/("CR")`
SR || OC ...[By converse of basic proportionality theorem]
Hence proved.
APPEARS IN
RELATED QUESTIONS
In figure, ∠BAC = 90º and segment AD ⊥ BC. Prove that AD2 = BD × DC.
Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
In ΔABC and ΔDEF, it is being given that: AB = 5 cm, BC = 4 cm and CA = 4.2 cm; DE=10cm, EF = 8 cm and FD = 8.4 cm. If AL ⊥ BC and DM ⊥ EF, find AL: DM.
E and F are the points in sides DC and AB respectively of parallelogram ABCD. If diagonal AC
and segment EF intersect at G; prove that:
State the SAS-similarity criterion
In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and AC is 14 cm. If arcs of equal radii 7 cm taking A, B, C and D as centres, have been drawn, then find the area of the shaded region ?

Figure shows Δ PQR in which ST || QR and SR and QT intersect each other at M. If `"PT"/"TR" = 5/3` find `("Ar" (triangle "MTS"))/("Ar" (triangle "MQR"))`

AD and BC are two straight lines intersecting at 0. CD and BA are perpendirulars from Band Con AD. If AB=6cm, CD =9cm, AD =20cm and BC=25cm, find the lengths of AO, BO, CO and DO.
The actual area of an island is 1872km2 . On a map, this area is 117 cm2. if the length of the coastline is 44cm on the map, find the length of its actual coastline.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : A' B', if AB = 4 cm.
The dimensions of the model of a multistorey building are 1.2 m × 75 cm × 2 m. If the scale factor is 1 : 30; find the actual dimensions of the building.
In the following figure, point D divides AB in the ratio 3 : 5. Find :
- `(AE)/(EC)`
- `(AD)/(AB)`
- `(AE)/(AC)`
Also, if: - DE = 2.4 cm, find the length of BC.
- BC = 4.8 cm, find the length of DE.

In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find : PQ

Let ∆ ABC ∽ ∆ DEF and their areas be respectively, 64 cm2 and 121 cm2. If EF = 15⋅4 cm, find BC.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 8cm, AB = 12cm and AE = 12cm, find CE.
In the figure, DE || AC and DC || AP. Prove that `"BE"/"EC" = "BC"/"CP"`
Find the scale factor in each of the following and state the type of size transformation:
Image length = 6cm, Actual length = 4cm.
A model of a ship is made to a scale of 1:500. Find: The area other deck o the ship, if the area of the deck of its model is m2
In a triangle ABC, AB = 4 cm, BC = 4.5 cm and CA = 5 cm. Construct ΔABC. Find the image A'B'C of the ΔABC obtained by enlarging it by a scale factor 2. Measure the sides of the image A'B'C' and show that AB:A'B' = AC:B'C' = CA:C'A'
Two triangles QPR and QSR, right angled at P and S respectively are drawn on the same base QR and on the same side of QR. If PR and SQ intersect at T, prove that PT × TR = ST × TQ
Construct a triangle similar to a given triangle LMN with its sides equal to `4/5` of the corresponding sides of the triangle LMN (scale factor `4/5 < 1`)
In the adjacent figure ∠BAC = 90° and AD ⊥ BC then

In any triangle _______ sides are opposite to equal angles
Two similar triangles will always have ________ angles
If ΔABC ~ ΔLMN and ∠A = 60° then ∠L = ?
Observe the figure and complete the following activity

In fig, ∠B = 75°, ∠D = 75°
∠B ≅ [ ______ ] ...[each of 75°]
∠C ≅ ∠C ...[ ______ ]
ΔABC ~ Δ [ ______ ] ...[ ______ similarity test]
In the given figure ΔABC ~ ΔPQR. The value of x is
 |
 |
If ΔABC ∼ ΔDEF and ∠A = 48°, then ∠D = ______.
Prove that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
Using the above theorem prove that a line through the point of intersection of the diagonals and parallel to the base of the trapezium divides the non-parallel sides in the same ratio.

In ΔABC, DE || BC (as shown in the figure), If AD = 4 cm, AB = 9 cm and AC = 13.5 cm, then the length of EC is ______.
